
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
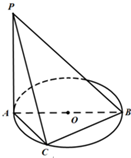 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
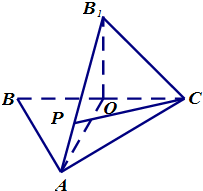 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
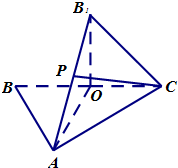 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.查看答案和解析>>
科目:高中数学 来源: 题型:
如图,有一个三角形的遮阳棚△ABC,AC=3m,BC=4m,AB=5m,
A,B是安置在地面上南北方向的两个定点,由正西方向的太
阳(用点O表示)射出的光线OCE与地面成30°的角,△ABE
为遮阳棚产生的阴影,当遮阳棚与地面构成60°的二面角时,
该遮阳棚所遮阴影△ABE的面积是______________

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省珠海市高三5月综合测试(二)理科数学试题 题型:解答题
如图(1), 是直径
是直径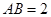 的圆上一点,
的圆上一点,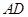 为圆O的切线,
为圆O的切线,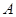 为切点,
为切点,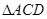 为等边三角形,连接
为等边三角形,连接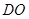 交
交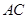 于
于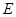 ,以
,以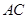 为折痕将
为折痕将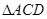 翻折到图(2)所示
翻折到图(2)所示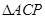 的位置,点P为平面ABC外的点.
的位置,点P为平面ABC外的点.
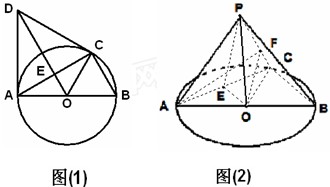
(1)求证:异面直线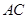 和
和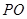 互相垂直;
互相垂直;
(2)若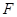 为
为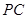 上一点,且
上一点,且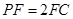 ,
,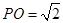 ,求三棱锥
,求三棱锥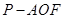 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com