
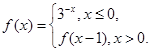 若
若 有且仅有三个解,则实数
有且仅有三个解,则实数 的取值范围是
的取值范围是| A.[1,2] | B.(-∞,2) | C.[1,+∞) | D.(-∞,1) |
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
 ,高
,高 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大 (高不变);二是高度增加
(高不变);二是高度增加 (底面直径不变)。
(底面直径不变)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用. )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.(1)(2)(4) | B.(4)(2)(3) | C.(4)(1)(3) | D.(4)(1)(2) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com