
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求 ![]() 的定义域;
的定义域;
(2)判断并证明 ![]() 的奇偶性.
的奇偶性.
【答案】
(1)解:由题意得, 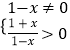
解得:﹣1<x<1,
∴原函数的定义域为(﹣1,1)
(2)解:f(x)在(﹣1,1)上为奇函数,证明如下,
∵f(﹣x)=loga ![]()
=loga( ![]() )﹣1
)﹣1
=﹣loga ![]()
=f(x);
∴f(x)在(﹣1,1)上为奇函数
【解析】(1)根据题意由真数大于零解出关于x的不等式即可。(2) 由奇函数的定义f(-x)=-f(x) ,代入验证即可得出结论。
【考点精析】本题主要考查了函数的定义域及其求法和函数的奇函数的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (x≠-2),h(x)=x2+1.
(x≠-2),h(x)=x2+1.
(1)求f(2),h(1)的值;
(2)求f[h(2)]的值;
(3)求f(x),h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ ![]() (k+1)x2+3kx+1,其中k∈R.
(k+1)x2+3kx+1,其中k∈R.
(1)当k=3时,求函数f(x)在[0,5]上的值域;
(2)若函数f(x)在[1,2]上的最小值为3,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)(理)求ξ的分布列和数学期望 (文)求P(ξ=1)的值
(3)(理)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,AB=AC=AA1 , AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 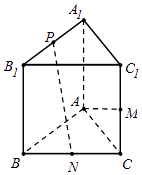
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数 ![]() 是偶函数,且满足
是偶函数,且满足 ![]() 上的解析式为
上的解析式为 ![]() ,过点
,过点 ![]() 作斜率为k的直线l , 若直线l与函数
作斜率为k的直线l , 若直线l与函数 ![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
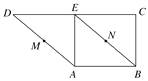
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com