
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,
,![]() 为函数
为函数![]() 的两个极值点,求证
的两个极值点,求证![]() .
.
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() .记
.记![]() 的前
的前![]() 项和为
项和为![]() ,并规定
,并规定![]() .定义集合
.定义集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)对数列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)给定正整数![]() .对所有满足
.对所有满足![]() 的数列
的数列![]() ,求集合
,求集合![]() 的元素个数的最小值.
的元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明朝的程大位在《算法统宗》中(1592年),有这么个算法歌诀:三人同行七十稀,五树梅花廿一枝,七子团圆正半月,除百零五便得知.它的意思是说:求某个数(正整数)的最小正整数值,可以将某数除以3所得的余数乘以70,除以5所得的余数乘以21,除以7所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止,所得结果就是这个数的最小正整数值.《孙子算经》上有一道极其有名的“物不知数”问题:“今有物不知其数,三三数之余二,五五数之余三,七七数之余二,问物几何.”用上面的算法歌诀来算,该物品最少是几件( )
A.21B.22C.23D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蜂巢是由工蜂分泌蜂蜡建成的从正面看,蜂巢口是由许多正六边形的中空柱状体连接而成,中空柱状体的底部是由三个全等的菱形面构成,菱形的一个角度是![]() ,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱
,这样的设计含有深刻的数学原理、我国著名数学家华罗庚曾专门研究蜂巢的结构著有《谈谈与蜂房结构有关的数学问题》.用数学的眼光去看蜂巢的结构,如图,在六棱柱![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 处分别用平面
处分别用平面![]() ,平面
,平面![]() ,平面
,平面![]() 截掉三个相等的三棱锥
截掉三个相等的三棱锥![]() ,
,![]() ,
,![]() ,平面
,平面![]() ,平面
,平面![]() ,平面
,平面![]() 交于点
交于点![]() ,就形成了蜂巢的结构.如图,以下四个结论①
,就形成了蜂巢的结构.如图,以下四个结论①![]() ;②
;②![]() ;③
;③![]() ,
,![]() ,
,![]() ,
,![]() 四点共面;④异面直线
四点共面;④异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .其中正确的个数是( ).
.其中正确的个数是( ).


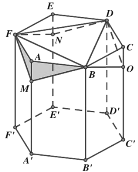
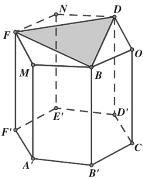
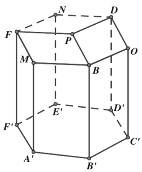
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,Q是抛物线上的一点,
的焦点为F,Q是抛物线上的一点,![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点![]() 作直线l与抛物线C交于M,N两点,在x轴上是否存在一点A,使得x轴平分
作直线l与抛物线C交于M,N两点,在x轴上是否存在一点A,使得x轴平分![]() ?若存在,求出点A的坐标,若不存在,请说明理由.
?若存在,求出点A的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,它是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.下图为国家统计局发布的2018年2月-2019年2月全国居民消费价格指数(CPI)数据折线图(注:同比是今年第n个月与去年第n个月之比;环比表示连续2个单位周期(比如连续两月)内的量的变化比,环比增长率=(本期数-上期数)/上期数×100%).
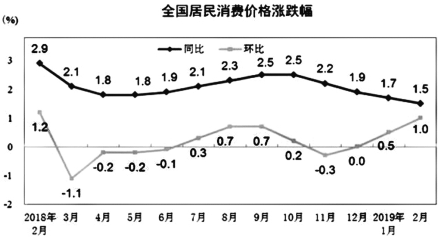
下列说法错误的是
A. 2019年2月份居民消费价格同比上涨1.5%B. 2019年2月份居民消费价格环比上涨1.0%
C. 2018年6月份居民消费价格环比下降0.1%D. 2018年11月份居民消费价格同比下降0.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“无桩有站”模式的公共自行车日益普及,即传统自行车加装智能锁,实现扫码租车及刷卡租车、某公司量产了甲、乙两种款式的公共自行车并投人使用,为了调查消费者对两种自行车的租赁情况,现随机抽取这两种款式的自行车各100辆,分别统计了每辆车在某周内的出租次数,得到甲、乙两种自行车这周内出租次数的频数分布表:
甲 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 20 | 25 | 25 | 10 | 20 |
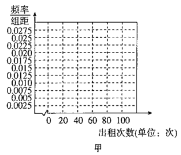
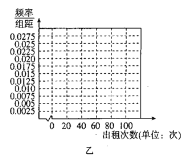
(1)根据频数分布表,完成上面频率分布直方图,并根据频率分布直方图比较甲、乙两种自行车这周内出租次数方差的大小(不必说明理由);
(2)如果两种自行车每次出租获得的利润相同,该公司决定大批量生产其中一种投入某城市使用,请你根据所学的统计知识,给出建议应该生产哪一种自行车,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点 .过点
.过点![]() 做两条相互垂直的直线
做两条相互垂直的直线![]() 、
、![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点.
四点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直线
,探究:直线![]() 是否过定点?若是,请求出定点坐标;若不是,请说明理由.
是否过定点?若是,请求出定点坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com