
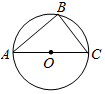
 如图所示,圆O的半径为R,A、B、C为圆O上不同的三点,圆心O在线段AC上.
如图所示,圆O的半径为R,A、B、C为圆O上不同的三点,圆心O在线段AC上.分析 (1)根据题意,求出圆O的面积与△ABC的面积,计算点P恰好位于△ABC内的概率值;
(2)建立适当的直角坐标系,求出对应△ABC的面积,计算点Q位于△ABC内的概率与取值范围.
解答 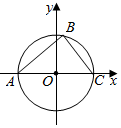 解:(1)记“所求点恰好位于△ABC内”为事件A,
解:(1)记“所求点恰好位于△ABC内”为事件A,
∵AC为原O的直径,
∴2R=$\sqrt{{4}^{2}{+3}^{2}}$=5,半径R=$\frac{5}{2}$,
∴圆O的面积为S圆O=π•${(\frac{5}{2})}^{2}$=$\frac{25π}{4}$;
又∵△ABC的面积为S△ABC=$\frac{1}{2}$×3×4=6,
∴点P恰好位于△ABC内的概率为
P(A)=$\frac{{S}_{△ABC}}{{S}_{圆O}}$=$\frac{6}{\frac{25π}{4}}$=$\frac{24}{25π}$;
(2)以O为原点,直线AC为x轴,以过O点并垂直于直线AC的直线为y轴建立直角坐标系,
则有A(-1,0),C(1,0),设B(x,y);
记“所取点Q位于△ABC内”为事件B,
则由题设知-1<x<1,R2=x2+y2=1,
∵$\overrightarrow{AB}$=(x+1,y),$\overrightarrow{CB}$=(x-1,y),
∴|$\overrightarrow{AB}$|=$\sqrt{{(x+1)}^{2}{+y}^{2}}$=$\sqrt{2+2x}$,
|$\overrightarrow{CB}$|=$\sqrt{{(x-1)}^{2}{+y}^{2}}$=$\sqrt{2-2x}$,
∴△ABC的面积为
S△ABC=$\frac{1}{2}$|AB|•|$\overrightarrow{CB}$|=$\frac{1}{2}$×$\sqrt{2+2x}$•$\sqrt{2-2x}$=$\frac{1}{2}$$\sqrt{4-{4x}^{2}}$;
又∵-1<x<1,∴0<4-4x2<4,
∴0<S△ABC<1;
又∵S圆O=π×12=π,
∴P(B)=$\frac{{S}_{△ABC}}{{S}_{圆O}}$,
∴点Q位于△ABC内的概率取值范围为0<P(B)<$\frac{1}{π}$.
点评 本题考查了几何概型的概率应用问题,解题时应求出对应几何图形的面积比值即可,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{3}$i | C. | -$\frac{1}{5}$ | D. | -$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>1} | B. | {x|x<-1或x>2} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个都是篮球 | B. | 至少有1个是气排球 | ||
| C. | 3个都是气排球 | D. | 至少有1个是篮球 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
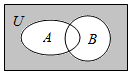 设全集U=R,集合A={x|-4<x<1},B={x|${4}^{x+\frac{1}{2}}$>$\frac{1}{8}$},则图中阴影部分所表示的集合为(-∞,-4].
设全集U=R,集合A={x|-4<x<1},B={x|${4}^{x+\frac{1}{2}}$>$\frac{1}{8}$},则图中阴影部分所表示的集合为(-∞,-4].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:选择题
在 上有一点
上有一点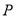 ,它到
,它到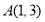 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点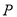 的坐标是( )
的坐标是( )
A.(-2,1) B.(1,2) C.(2,1) D.(-1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com