
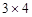 棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从
棋盘,规定每次只能沿正方形的边运动,且只能走一个单位,则从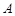 走到
走到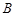 的最短路径的走法有 种
的最短路径的走法有 种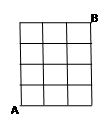
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源:不详 题型:单选题
| A.24 | B.36 | C.720 | D.1000 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
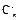 +2
+2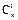 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为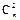 +22
+22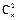 =
=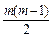 +2n(n-1)=
+2n(n-1)=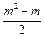 +(11-m)(
+(11-m)(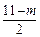 -1)=(m-
-1)=(m-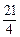 )2+
)2+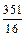 .
. 33,
33,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com