
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为1?若存在,求出
上的最小值为1?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .极小值
.极小值![]() ,无极大值.(2)存在实数
,无极大值.(2)存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
【解析】试题分析:(1)先求导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值(2)先根据导函数是否变化分类讨论:当![]() 时,导函数恒为正,所以最小值为
时,导函数恒为正,所以最小值为![]() ;当
;当![]() 时,导函数先负后正,所以最小值为
时,导函数先负后正,所以最小值为![]() ;当
;当![]() 时,导函数为负,最小值为
时,导函数为负,最小值为![]() ,最后根据最小值为1,解对应
,最后根据最小值为1,解对应![]() 的值。
的值。
试题解析:解:由题意知函数的定义域为![]() ,
,![]() .
.
(Ⅰ)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
所以当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(Ⅱ)①当![]() 时,函数
时,函数![]() 在
在![]() 为增函数,
为增函数,
∴函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,显然
,显然![]() ,故不满足条件;
,故不满足条件;
②当![]() 时,函数
时,函数![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数
上为增函数
故函数![]() 在
在![]() 上的最小值为
上的最小值为![]() 的极小值
的极小值![]() ,
,
即![]() ,满足条件;
,满足条件;
③当![]() 时,函数
时,函数![]() 在
在![]() 为减函数,
为减函数,
故函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,即
,即![]() ,不满足条件.
,不满足条件.
综上所述,存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ) 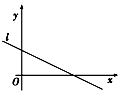
A.已知购买一张彩票中奖的概率为 ![]() ,则购买1000张这种彩票一定能中奖
,则购买1000张这种彩票一定能中奖
B.互斥事件一定是对立事件
C.如图,直线l是变量x和y的线性回归方程,则变量x和y相关系数在﹣1到0之间
D.若样本x1 , x2 , …xn的方差是4,则x1﹣1,x2﹣1,…xn﹣1的方差是3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |

(1)试由图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在[45,55)和[55,65)的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在[25,35)和[45,55)两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户准备建一个水平放置的直四棱柱形储水器(如图),其中直四棱柱的高![]() ,两底面
,两底面![]() 是高为
是高为![]() ,面积为
,面积为![]() 的等腰梯形,且
的等腰梯形,且![]() ,若储水窖顶盖每平方米的造价为100元,侧面每平方米的造价为400元,底部每平方米的造价为500元.
,若储水窖顶盖每平方米的造价为100元,侧面每平方米的造价为400元,底部每平方米的造价为500元.


(1)试将储水窖的造价![]() 表示为
表示为![]() 的函数;
的函数;
(2)该农户如何设计储水窖,才能使得储水窖的造价最低,最低造价是多少元?(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生态公园的平面图呈长方形(如图),已知生态公园的长AB=8(km),宽AD=4(km),M,N分别为长方形ABCD边AD,DC的中点,P,Q为长方形ABCD边AB,BC(不含端点)上的一点.现公园管理处拟修建观光车道P﹣Q﹣N﹣M﹣P,要求观光车道围成四边形(如图阴影部分)的面积为15(km2),设BP=x(km),BQ=y(km), 
(1)试写出y关于x的函数关系式,并求出x的取值范围;
(2)若B为公园入口,P,Q为观光车站,观光车站P位于线段AB靠近入口B的一侧.经测算,每天由B入口至观光车站P,Q乘坐观光车的游客数量相等,均为1万人,问如何确定观光车站P,Q的位置,使所有游客步行距离之和最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现要在边长为100m的正方形ABCD内建一个交通“环岛”.以正方形的四个顶点为圆心在四个角分别建半径为xm(x不小于9)的扇形花坛,以正方形的中心为圆心建一个半径为 ![]() m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m.
m的圆形草地.为了保证道路畅通,岛口宽不小于60m,绕岛行驶的路宽均小于10m. 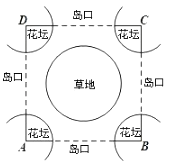
(1)求x的取值范围;(运算中 ![]() 取1.4)
取1.4)
(2)若中间草地的造价为a元/m2 , 四个花坛的造价为 ![]() 元/m2 , 其余区域的造价为
元/m2 , 其余区域的造价为 ![]() 元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
元/m2 , 当x取何值时,可使“环岛”的整体造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为(2﹣m)x+(2m+1)y+3m+4=0,其中m∈R.
(1)求证:直线l恒过定点;
(2)当m变化时,求点P(3,1)到直线l的距离的最大值;
(3)若直线l分别与x轴、y轴的负半轴交于A,B两点,求△AOB面积的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com