
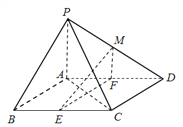
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析:(Ⅰ)线面垂直的证明,往往利用线面垂直判定定理,即从线线垂直出发给予证明,而线线垂直的寻找与论证,一般从两个方面,一是利用平几知识,如本题经解三角形可得![]() ,再根据中点条件得平行条件,从而可得
,再根据中点条件得平行条件,从而可得![]() .二是利用线面位置关系有关定理进行转化,如本题利用面面垂直的性质定理可得线面垂直,再根据线面垂直性质定理可得线线垂直.(Ⅱ)解决有关线面角的问题,一般利用空间向量数量积进行处理比较方便,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据向量数量积求出直线向量与法向量夹角余弦值,最后根据线面角与向量夹角之间关系列等量关系,求出比值.
.二是利用线面位置关系有关定理进行转化,如本题利用面面垂直的性质定理可得线面垂直,再根据线面垂直性质定理可得线线垂直.(Ⅱ)解决有关线面角的问题,一般利用空间向量数量积进行处理比较方便,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出面的法向量,再根据向量数量积求出直线向量与法向量夹角余弦值,最后根据线面角与向量夹角之间关系列等量关系,求出比值.
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() .由
.由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() ,
,
所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() 底面
底面![]() ,
, ![]() ,所以
,所以![]() 两两垂直,
两两垂直,
以![]() 分别为
分别为![]() 、
、![]() 、
、![]() ,建立空间直角坐标系,
,建立空间直角坐标系,
则![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
, ![]() ,易得平面
,易得平面![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
, ![]() ,得
,得![]()
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即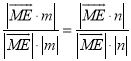 ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 综上所得:
(舍). 综上所得: ![]()


科目:高中数学 来源: 题型:
【题目】某单位举行联欢活动,每名职工均有一次抽奖机会,每次抽奖都是从甲箱和乙箱中各随机摸取1个球,已知甲箱中装有3个红球,5个绿球,乙箱中装有3个红球,3个绿球,2个黄球.在摸出的2个球中,若都是红球,则获得一等奖;若都是绿球,则获得二等奖;若只有1个红球,则获得三等奖;若1个绿球和1个黄球,则不获奖.
(1)求每名职工获奖的概率;
(2)设X为前3名职工抽奖中获得一等奖和二等奖的次数之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比为正整数的等比数列,{bn}是等差数列,且a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
(1)求数列{an}和{bn}的通项公式;
(2)设pn= ![]() ,数列{pn}的前n项和为Sn .
,数列{pn}的前n项和为Sn .
①试求最小的正整数n0 , 使得当n≥n0时,都有S2n>0成立;
②是否存在正整数m,n(m<n),使得Sm=Sn成立?若存在,请求出所有满足条件的m,n;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
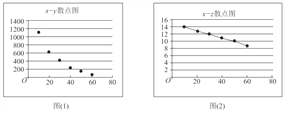
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: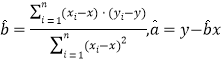 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , a2=4,S5=30
(1)求数列{an}的通项公式an
(2)设数列{ ![]() }的前n项和为Tn , 求证:
}的前n项和为Tn , 求证: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.

(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: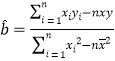 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a4=7,a10=19,其前n项和为Sn .
(1)求数列{an}的通项公式an及Sn;
(2)若等比数列{bn}的前n项和为Tn , 且b1=2,b4=S4 , 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com