
【题目】如图,点P是菱形ABCD所在平面外一点,且![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() .
.
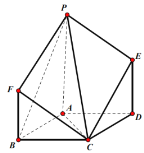
(1)求证:平面![]() 平面PCE;
平面PCE;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取PC中点M,连接BD交AC于O,连接OM,EM.根据菱形性质可得![]() ,再由
,再由![]() 即可证明
即可证明![]() 平面PAC,进而利用平行四边形性质可证明
平面PAC,进而利用平行四边形性质可证明![]() ,即可得
,即可得![]() 平面PAC,结合平面与平面垂直的判定即可证明平面
平面PAC,结合平面与平面垂直的判定即可证明平面![]() 平面
平面![]() ;
;
(2)以OB,OC,OM所在直线分别为x轴,y轴,z轴建立空间直角坐标系,由题意可设![]() ,写出各个点的坐标.利用向量的数量积求得平面
,写出各个点的坐标.利用向量的数量积求得平面![]() 和
和
平面![]() 的法向量,即可利用空间向量数量积的运算求得夹角的余弦值.
的法向量,即可利用空间向量数量积的运算求得夹角的余弦值.
(1)证明:取PC中点M,连接BD交AC于O,连接OM,EM.如下图所示:
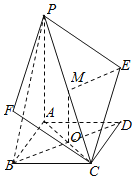
在菱形ABCD中,![]() ,
,
![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() ,
,
又![]() ,PA,
,PA,![]() 平面PAC,
平面PAC,
![]() 平面PAC,
平面PAC,
![]() ,M分别是AC,PC的中点,
,M分别是AC,PC的中点,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形OMED是平行四边形,则
四边形OMED是平行四边形,则![]() ,
,
![]() 平面PAC,
平面PAC,
又![]() 平面PCD,
平面PCD,
![]() 平面
平面![]() 平面PCE.
平面PCE.
(2)由(1)得![]() 平面PAC﹐则OB,OC,OM两两垂直,以OB,OC,OM所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如下图所示
平面PAC﹐则OB,OC,OM两两垂直,以OB,OC,OM所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如下图所示
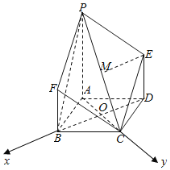
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设![]() 是平面BPC的一个法向量,则
是平面BPC的一个法向量,则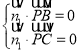 ,即
,即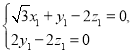 ,
,![]() ,
,
设![]() 是平面FPC的一个法向量,同理得,
是平面FPC的一个法向量,同理得,![]()
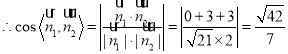 ,
,
由图可知二面角![]() 为锐二面角
为锐二面角
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某电视台举行一个比赛类型的娱乐节目,A、B两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将A队第六位选手的成绩没有给出,并且告知大家B队的平均分比A队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
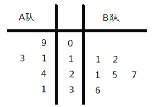
(1)根据茎叶图中的数据,求出A队第六位选手的成绩;
(2)主持人从A队所有选手成绩中随机抽取2个,求至少有一个为“晋级”的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(Ⅰ)写出直线l普通方程和曲线C的直角坐标方程;
(Ⅱ)过点M(-1,0)且与直线l平行的直线l1交C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() ,
,![]() ,设圆C的半径为1,圆心在
,设圆C的半径为1,圆心在![]() 上.
上.
(1)若圆心C也在直线![]() 上,①求圆C的方程;
上,①求圆C的方程;
②过点![]() 作圆C的切线,求切线的方程;
作圆C的切线,求切线的方程;
(2)若圆在直线![]() 截得的弦长为
截得的弦长为![]() ,求圆C的方程.
,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,且
,且![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 中点为坐标原点建立平面直角坐标系.
中点为坐标原点建立平面直角坐标系.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知定点![]() ,不垂直于
,不垂直于![]() 的动直线
的动直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,若直线
两点,若直线![]()
![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到![]() 的图象
的图象![]() ,只要将
,只要将![]() 图象
图象![]() 怎样变化得到( )
怎样变化得到( )
A.将![]() 的图象
的图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
B.将![]() 的图象
的图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
C.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向右平移
沿x轴方向向右平移![]() 个单位
个单位
D.先作![]() 关于x轴对称图象
关于x轴对称图象![]() ,再将图象
,再将图象![]() 沿x轴方向向左平移
沿x轴方向向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十三届全国人大二次会议于2019年3月5日在京召开为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从全校学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 80 | 40 |
女生 | 30 | 30 |
(1)根据上表说明,在犯错误的概率不超过1%的前提下,能否认为该校大学生收看开幕会与性别有关?(计算结果精确到0.001)
(2)现从随机抽取的学生中,采用按性别分层抽样的方法选取6人,来参加2019年两会的志愿者宣传活动,若从这6人中随机选取2人到各班级宣传介绍,求恰好选到一名男生和一名女生的概率. 附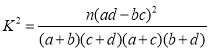 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y=![]() ,D为直线y=
,D为直线y=![]() 上的动点,过D作C的两条切线,切点分别为A,B.
上的动点,过D作C的两条切线,切点分别为A,B.
(1)证明:直线AB过定点:
(2)若以E(0,![]() )为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
)为圆心的圆与直线AB相切,且切点为线段AB的中点,求四边形ADBE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com