【题目】重庆某地区
年至
年农村居民家庭人均纯收入
（单位：万元）的数据如表：
年份 |
|
|
|
|
|
年份代号 |
|
|
|
|
|
纯收入 |
|
|
|
|
|
（1）求关于
的线性回归方程；
（2）利用（1）中的回归方程，分析年至年该地区农村居民家庭人均纯收入的变化情况，并预测该地区
年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：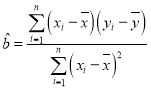
，
.
科目：高中数学 来源： 题型：
【题目】将一枚质地均匀的硬币向上抛掷三次，下列两个事件中，是对立事件的是（ ）
A.事件
：“恰有两次正面向上”，事件
：“恰有两次反面向上”
B.事件
：“恰有两次正面向上”，事件
：“恰有一次正面向上”
C.事件
：“至少有一次正面向上”，事件
：“至多一次正面向上”
D.事件
：“至少有一次正面向上”，事件
：“恰有三次反面向上”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】椭圆C:
(a>b>0)的左、右焦点分别为
，离心率为
，过焦点
且垂直于x轴的直线被椭圆C截得的线段长为1．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知点M（0，-1），直线l经过点N（2，1）且与椭圆C相交于A,B两点（异于点M），记直线MA的斜率为
，直线MB的斜率为
，证明
为定值，并求出该定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
名学生某次数学考试成绩（单位：分）的频率分布直方图如图.
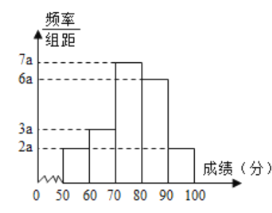
（1）求频率分布直方图中
的值；
（2）估计总体中成绩落在
中的学生人数；
（3）根据频率分布直方图估计名学生数学考试成绩的众数，中位数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，曲线
过点
，其参数方程为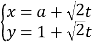
（
为参数， 
），以
为极点， 
轴非负半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线
的普通方程和曲线
的直角坐标方程；
（2）求已知曲线
和曲线
交于
两点，且
，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知{an}为正项等比数列，a1+a2=6，a3=8．
（1）求数列{an}的通项公式an；
（2）若bn=
，且{bn}前n项和为Tn，求Tn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4—4：坐标系与参数方程]
在直角坐标系
中，曲线
的方程为
．以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）求的直角坐标方程；
（2）若与有且仅有三个公共点，求的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点
是直线
（
）上一动点， 
、
是圆
： 
的两条切线， 
、
为切点， 
为圆心，若四边形
面积的最小值是
，则
的值是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】∵圆的方程为： 
，
∴圆心C(0,1)，半径r=1.
根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,切线长PA,PB最小。切线长为4，
∴
，
∴圆心到直线l的距离为
.
∵直线
（
），
∴
,解得
，由
所求直线的斜率为
故选D.
【题型】单选题
【结束】
19
【题目】抛物线
的焦点为
，准线为
，经过
且斜率为
的直线与抛物线在
轴上方的部分相交于点
， 
，垂足为
，则
的面积是 （ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
