
【题目】在一次演唱会上共10 名演员(每名演员都会唱歌或跳舞),其中7人能唱歌,6人会跳舞.
(1)问既能唱歌又会跳舞的有几人?
(2)现要选出一个2人唱歌2人伴舞的节目,有多少种选派方法?
科目:高中数学 来源: 题型:
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面是菱形的四棱锥![]() 中,
中,![]() .
.
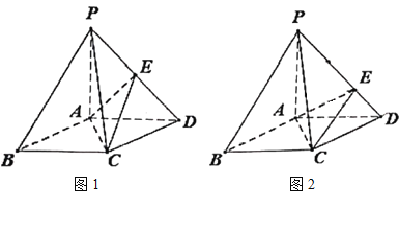
(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上.
上.
①如图1,若点![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
②如图2,若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
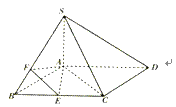
【题目】如图所示,四棱锥S﹣ABCD中,四边形ABCD为平行四边形,BA⊥AC,SA⊥AD,SC⊥CD.
(Ⅰ)求证:AC⊥SB;
(Ⅱ)若AB=AC=SA=3,E为线段BC的中点,F为线段SB上靠近B的三等分点,求直线SC与平面AEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,直线l的极坐标方程为ρcosθ=4,曲线C的极坐标方程为ρ=2cosθ+2sinθ,以极点为坐标原点O,极轴为x轴的正半轴建立直角坐标系,射线l':y=kx(x≥0,0<k<1)与曲线C交于O,M两点.
(Ⅰ)写出直线l的直角坐标方程以及曲线C的参数方程;
(Ⅱ)若射线l′与直线l交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水.已知该厂生活用水为每小时10吨,生产用水量![]() (吨)与时间
(吨)与时间![]() (单位:小时,且规定早上6时
(单位:小时,且规定早上6时![]() )的函数关系式为:
)的函数关系式为:![]() ,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
(1)若进水量选择为![]() 级,水塔中剩余水量为
级,水塔中剩余水量为![]() 吨,试写出
吨,试写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何选择进水量,既能始终保证该厂的用水(水塔中水不空)又不会使水溢出?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com