
【题目】已知函数![]() .
.
(1)若![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,
,![]() ,
,![]() 是
是![]() 的三个零点,且
的三个零点,且![]() .当
.当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)求导得到![]() ,设
,设![]() ,得到
,得到![]() ,从而得到
,从而得到![]() 的单调性和
的单调性和![]() ,根据
,根据![]() 有两个极值点,结合零点存在定理,得到
有两个极值点,结合零点存在定理,得到![]() 的范围;(2)当
的范围;(2)当![]() 时,可知
时,可知![]() 单调递增,不符合题意,当
单调递增,不符合题意,当![]() 时,得到
时,得到![]() ,记
,记![]() ,利用导数求出
,利用导数求出![]() 的单调性,从而确定
的单调性,从而确定![]() 的两根的范围,结合
的两根的范围,结合![]() 的范围,得到
的范围,得到![]() 的范围,从而得证.
的范围,从而得证.
(1)![]() ,
,
![]() ,
,
设![]()
![]()
![]() 时,
时,![]() ,所以
,所以![]() 单调递减,即
单调递减,即![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,所以
,所以![]() 单调递增,即
单调递增,即![]() 单调递增;
单调递增;
所以![]() ,
,
因为![]() 有两个极值点,所以
有两个极值点,所以
![]() 有两个解,
有两个解,
所以![]() ,即
,即![]() ,
,
又因为![]() 和
和![]() 时,都有
时,都有![]() ,
,
所以![]() 即为所求..
即为所求..
(2)证明:(ⅰ)当![]() ,由(1)可知
,由(1)可知
![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 至多一个零点,与条件矛盾,
至多一个零点,与条件矛盾,
所以![]() .
.
(ⅱ)当![]() 时,由(1)可知:
时,由(1)可知:![]() ,
,
![]() 时
时![]() 单调递增;
单调递增;
![]() 时
时![]() 单调递减.
单调递减.
因为![]() ,所以
,所以![]() .
.
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
记![]() ,则
,则![]() 、
、![]() 是
是![]() 的两根.
的两根.
![]() ,
,
记![]() ,
,
则![]() .
.
易知![]() 和
和![]() 时,都有
时,都有![]() ,又
,又![]() ,
,
所以![]() 在
在![]() 上单调递增..
上单调递增..
又因为![]() ,
,
所以![]() 时,
时,![]() ,
,
即![]() ,所以
,所以![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,
即![]() ,
,![]() 单调递增,
单调递增,
设![]() 的两根为
的两根为![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() .
.
当![]() 时,
时,![]() 的两根
的两根![]() 、
、![]() 满足
满足![]() ,
,
则![]() ,证毕.
,证毕.


科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
![]()
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:

(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为![]() ,求
,求![]() 的数学期望与方差.
的数学期望与方差.
参考公式:
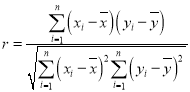 ,
,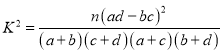 ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相交.
线性相交.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图三棱锥A-BCD中,BD⊥CD,E,F分别为棱BC,CD上的点,且BD∥平面AEF,AE⊥平面BCD.
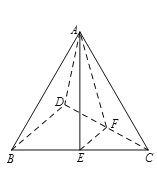
(1)求证:平面AEF⊥平面ACD;
(2)若![]() ,
,![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
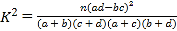 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com