
【题目】曲线y=1+![]() 与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
与直线y=k(x-2)+4有两个交点,则实数k的取值范围是( )
A. (![]() ,+∞)B. (
,+∞)B. (![]() ,
,![]() ]C. (0,
]C. (0,![]() )D. (
)D. (![]() ,
,![]() ]
]
科目:高中数学 来源: 题型:
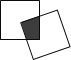
【题目】现有一个关于平面图形的命题:如图,同一平面内有两个边长都是2的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知函数f(x)![]() (2x
(2x![]() ),若f(
),若f(![]() )
)![]() ,θ∈(0,
,θ∈(0,![]() ),求tanθ.
),求tanθ.
(2)若函数g(x)=﹣(![]() sin
sin![]() cos
cos![]() )cos
)cos![]() ,讨论函数g(x)在区间[
,讨论函数g(x)在区间[![]() ,
,![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为AB、BC的中点,现在沿DE、DF及EF把△ADE、△CDF和△BEF折起,使A、B、C三点重合,重合后的点记为P.

问:(1)这个几何体是什么?
(2)这个几何体由几个面构成?每个面的三角形是什么三角形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分两层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2:
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 | x | 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
(1)求x,y的值;
(2)在答题纸上完成频率分布直方图;并根据频率分布直方图,估计该工厂B类工人生产能力的平均数(同一组中的数据用该区间的中点值作代表)和中位数.(结果均保留一位小数)


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列所给4个图象中,与所给3件事吻合最好的顺序为 ( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速;
(3)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间.
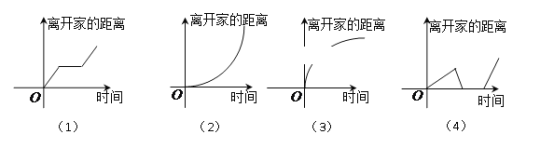
A. (1)(2)(4) B. (4)(2)(1) C. (4)(3)(1) D. (4)(1)(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
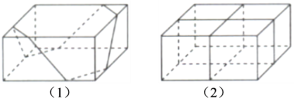
【题目】春节期间,佳怡准备去探望奶奶,她到商店买了一盒点心.为了美观起见,售货员对点心盒做了一个捆扎(如图(1)所示),并在角上配了一个花结.售货员说,这样的捆扎不仅漂亮,而且比一般的十字捆扎(如图(2)所示)包装更节省彩绳.你同意这种说法吗?请给出你的理由.(注;长方体点心盒的高小于长、宽.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com