练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知方程x2+my2=1表示焦点在y轴上的椭圆，则m的取值范围是（　　）
    A．m＜1B．-1＜m＜1C．m＞1D．0＜m＜1

    分析 根据题意，将方程变形为$\frac{{y}^{2}}{\frac{1}{m}}$+$\frac{{x}^{2}}{1}$=1，由椭圆的标准方程分析可得$\frac{1}{m}$＞1，解可得m的取值范围，即可得答案．

    解答 解：根据题意，方程x2+my2=1变形可得：$\frac{{y}^{2}}{\frac{1}{m}}$+$\frac{{x}^{2}}{1}$=1，
    若其表示焦点在y轴上的椭圆，
    则有$\frac{1}{m}$＞1，
    解可得0＜m＜1；
    故选：D．

    点评 本题考查椭圆的标准方程，关键是掌握椭圆的标准方程的形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    18．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-x，x＞0}\\{1-|2x+1|，x≤0}\end{array}\right.$，若关于x的方程f（x）=kx-1有两个不相等的实数根，则实数k的取值范围为{k|k≥2或k=1}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设函数f（x）为R上的增函数，求证：a+b＜0的充要条件是f（a）+f（b）＜f（-a）+f（-b）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．设函数f（x）=$\left\{\begin{array}{l}{-4{x}^{2}，x＜0}\\{{x}^{2}-x，x≥0}\end{array}\right.$，若f（a）=-$\frac{1}{4}$，则a=$\frac{1}{4}$或$\frac{1}{2}$，若方程f（x）-b=0有三个不同的实根，则实数b的取值范围是（-$\frac{1}{4}$，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．“an+1an-1=an2，n≥2且n∈N”是“数列{an}为等比数列”的（　　）
    A．必要不充分条件B．充分不必要条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

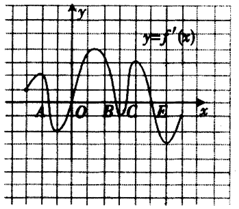    15．函数y=f（x）定义在区间（-3，7）上，其导函数如图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知a，b，c分别为△ABC的内角A，B，C的对边，且acosC+（c-2b）cosA=0．
    （Ⅰ）求A；
    （Ⅱ）若a=2，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知集合P={x|1≤x≤3}，Q={x|（x-1）2≤4}，则P∩Q=（　　）
    A．[-1，3]B．[1，3]C．[1，2]D．（-∞，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB=2，AD=DC=1，图中圆弧所在圆的圆心为点C，半径为$\frac{1}{2}$，且点P在图中阴影部分（包括边界）运动．若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$，其中x，y∈R，则4x-y的最大值为（　　）
    A．$3-\frac{{\sqrt{2}}}{4}$B．$3+\frac{{\sqrt{5}}}{2}$C．2D．$3+\;\frac{{\sqrt{17}}}{2}$

    查看答案和解析>>

    同步练习册答案