
【题目】现有4个人参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1) 求出4个人中恰有2个人去 参加甲游戏的概率;
(2)求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率;
(3)用![]() 分别表示这4个人中去参加甲、乙游戏的人数,记
分别表示这4个人中去参加甲、乙游戏的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
【答案】(1)8:27
(2)1:9
(3) ![]() 的分布列是
的分布列是
| 0 | 2 | 4 |
|
|
|
|
![]()
【解析】试题分析:依题意,这4个人中,每个人去参加甲游戏的概率为![]() ,去参加乙游戏的人数的概率为
,去参加乙游戏的人数的概率为![]() 设“这4个人中恰有i人去参加甲游戏”为事件
设“这4个人中恰有i人去参加甲游戏”为事件![]() ,故
,故![]() ;(Ⅰ)这4个人中恰有2人去参加甲游戏的概率为P(A2);(Ⅱ)设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B,则B=A3∪A4,利用互斥事件的概率公式可求;(Ⅲ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
;(Ⅰ)这4个人中恰有2人去参加甲游戏的概率为P(A2);(Ⅱ)设“这4个人中去参加甲游戏的人数大于去参加乙游戏”为事件B,则B=A3∪A4,利用互斥事件的概率公式可求;(Ⅲ)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
试题解析:解:依题意,这4个人中,每个人去参加甲游戏的概率为![]() ,去参加乙游戏的概率为
,去参加乙游戏的概率为![]() .设“这4个人中恰有i人去参加甲游戏”为事件
.设“这4个人中恰有i人去参加甲游戏”为事件![]() (i=0,1,2,3,4),则
(i=0,1,2,3,4),则![]()
(Ⅰ)这4个人中恰有2人去参加甲游戏的概率![]() 3分
3分
(Ⅱ)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则![]() ,
,
由于![]() 与
与![]() 互斥,故
互斥,故![]()
所以,这4个人去参加甲游戏的人数大于去参加乙游戏的人数的概率为![]() 7分
7分
(Ⅲ)ξ的所有可能取值为0,2,4.由于![]() 与
与![]() 互斥,
互斥,![]() 与
与![]() 互斥,故
互斥,故
![]() ,
,![]()
![]() 。
。
所以ξ的分布列是
ξ | 0 | 2 | 4 |
P |
|
|
|
随机变量ξ的数学期望![]() 12分.
12分.


科目:高中数学 来源: 题型:
【题目】袋中装有大小形状完全相同的5个小球,其中3个白球的标号分别为1、 2 、3, 2 个黑球的标号分别为1、3.
(Ⅰ)从袋中随机摸出两个球,求摸到的两球颜色与标号都不相同的概率;
(Ⅱ)从袋中有放回地摸球,摸两次,每次摸出一个球,求摸出的两球的标号之和小于4 的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题13分)已知函数f(x)=![]() -
-![]() (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[![]() ,2]上的值域是[
,2]上的值域是[![]() ,2],求a的值.
,2],求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
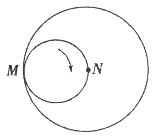
【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点。那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为
,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为 ![]()
(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M, ![]() =λ(
=λ( ![]() ),若点N在圆O上,求正实数λ的取值范围.
),若点N在圆O上,求正实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设动点![]() 是圆
是圆![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,若点
,若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,若直线
,若直线![]() ,
, ![]() 的斜率之和为定值3,求证:直线
的斜率之和为定值3,求证:直线![]() 必经过定点,并求出该定点的坐标.
必经过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,销售每吨乙产品可获得利润3万元。该企业在一个生产周期消耗A原料不超过13吨,B原料不超过18吨。问该企业如何安排可获得最大利润,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线顶点在原点,焦点在![]() 轴上,又知此抛物线上一点
轴上,又知此抛物线上一点![]() 到焦点的距离为6.
到焦点的距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 中点横坐标为2,求
中点横坐标为2,求![]() 的值.
的值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】试题分析:
(1)由题意设抛物线方程为![]() ,则准线方程为
,则准线方程为![]() ,解得
,解得![]() ,即可求解抛物线的方程;
,即可求解抛物线的方程;
(2)由![]() 消去
消去![]() 得
得![]() ,根据
,根据![]() ,解得
,解得![]() 且
且![]() ,得到
,得到![]() ,即可求解
,即可求解![]() 的值.
的值.
试题解析:
(1)由题意设抛物线方程为![]() (
(![]() ),其准线方程为
),其准线方程为![]() ,
,
∵![]() 到焦点的距离等于
到焦点的距离等于![]() 到其准线的距离,∴
到其准线的距离,∴![]() ,∴
,∴![]() ,
,
∴此抛物线的方程为![]() .
.
(2)由![]() 消去
消去![]() 得
得![]() ,
,
∵直线![]() 与抛物线相交于不同两点
与抛物线相交于不同两点![]() 、
、![]() ,则有
,则有![]()
解得![]() 且
且![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴所求![]() 的值为2.
的值为2.
【题型】解答题
【结束】
20
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果三棱锥![]() 的体积为
的体积为![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆的两个焦点分别为![]() ,
, ![]() ,过
,过![]() 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点![]() ,若
,若![]() 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】试题分析:解:设点P在x轴上方,坐标为(![]() ),∵
),∵![]() 为等腰直角三角形,∴|PF2|=|F1F2|,
为等腰直角三角形,∴|PF2|=|F1F2|, ![]() ,故选D.
,故选D.
考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系
【题型】单选题
【结束】
8
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com