
(1)现有可围36米长的钢筋材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为24 m2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋总长度最小?
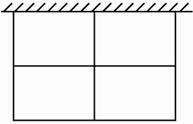
图3-4-2
解:(1)设每间虎笼长为x米,宽为 y米,则由条件知4x+6y=36,即2x+3y=18.
设每间虎笼的面积为S,则S=xy.
方法一:由于2x+3y≥![]() ,
,
∴![]() ≤18,得xy≤
≤18,得xy≤![]() ,即S≤
,即S≤![]() .
.
当且仅当2x=3y时等号成立.
由![]() 解得
解得![]()
故每间虎笼长为4.5 m,宽为3 m时,可使面积最大.
方法二:由2x+3y=18,得x=9-![]() y.
y.
∵x>0,∴0<y<6.
S=xy=(9-![]() y)y=
y)y=![]() (6-y)y.
(6-y)y.
∵0<y<6,∴6-y>0.
∴S≤![]() [
[![]() ]2=
]2=![]() .
.
当且仅当6-y=y,即y=3时,等号成立,此时x =4.5.故每间虎笼长4.5 m,宽3 m时,可使面积最大.
(2)由条件知S=xy=24.
设钢筋网总长为l,则l=4x+6y.
方法一:∵2x+3y≥![]() =24,
=24,
∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y时等号成立.
由![]() 解得
解得![]()
故每间虎笼长6 m,宽4 m,可使钢筋网总长最小.
方法二:由xy=24,得x=![]() .
.
∴l=4x+6y=![]() +6y=6(
+6y=6(![]() +y)≥6×
+y)≥6×![]() =48,
=48,
当且仅当![]() =y,即y=4时,等号成立,此时x=6.
=y,即y=4时,等号成立,此时x=6.
故每间虎笼长6 m,宽4 m时,可使钢筋总长最小.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
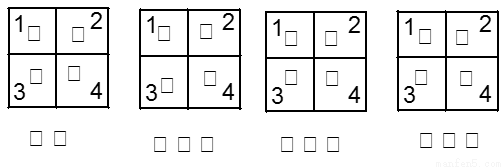
11、四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2009次互换座位后,小兔的座位对应的是( )
| |||||||||||||||||||||||||||||||||||||||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:广东省深圳高级中学2011-2012学年高二上学期期末数学文科试题 题型:013
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2005次互换座位后,小兔的座位对应的是

编号1
编号2
编号3
编号4
查看答案和解析>>
科目:高中数学 来源:2013届广东省实验学校高二下期中理科数学试卷A(解析版) 题型:选择题
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2005次互换座位后,小兔的座位对应的是( )
A、编号1 B 、编号2 C、 编号3 D、 编号4
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市2010届高二下学期期中考试(文科) 题型:选择题
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排
动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2005次互换座位后,
小兔的座位对应的是 ( )
 |
A.编号1 B.编号2 C.编号3 D.编号4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com