
【题目】下列说法正确的个数为( )
①“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
②若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
③在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
④已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .
.
A.4B.3C.2D.1
【答案】C
【解析】
根据复合命题真假即可判断①;根据平均数的计算公式可判断②;对于③由辅助角公式化简三角函数式,结合正弦函数的图像与性质即可求得![]() 的
的![]() 取值范围,进而由几何概型概率计算得解;对于④根据正态分布曲线的性质,即可求得概率.
取值范围,进而由几何概型概率计算得解;对于④根据正态分布曲线的性质,即可求得概率.
对于①,由复合命题“![]() 为真”,可知
为真”,可知![]() 为真,或
为真,或![]() 为真;若“
为真;若“![]() 为真”,则
为真”,则![]() 为真,且
为真,且![]() 为真.所以“
为真.所以“![]() 为真”是“
为真”是“![]() 为真”的必要不充分条件,所以①错误;
为真”的必要不充分条件,所以①错误;
对于②,若数据![]() 的平均数为1,由平均数公式可知
的平均数为1,由平均数公式可知![]() 的平均数为2,所以②正确;
的平均数为2,所以②正确;
对于③,在区间![]() 上.若
上.若![]() ,解得
,解得![]() .
.
则在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为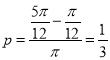 ,所以③错误;
,所以③错误;
对于④,随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.
![]() ,由正态分布曲线规律可知
,由正态分布曲线规律可知
![]() ,所以④正确.
,所以④正确.
综上可知,正确的为②④
故选:C


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() 是曲线段
是曲线段![]() :
:![]() (
(![]() 是参数,
是参数,![]() )的左、右端点,
)的左、右端点,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
(1)建立适当的极坐标系,写出点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() ,
, ![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 和圆
和圆![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
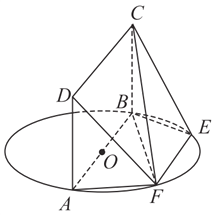
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆
,圆![]() ,点
,点![]() 为圆
为圆![]() 上动点,线段
上动点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 与
与![]() 作平行直线
作平行直线![]() 和
和![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
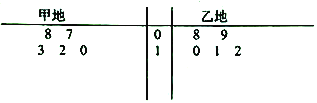
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实数,已知函数
为实数,已知函数![]() 的导函数为
的导函数为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 为实数,若对于任意
为实数,若对于任意![]() ,不等式
,不等式![]() 恒成立,且存在唯一的实数
恒成立,且存在唯一的实数![]() 使得
使得![]() 成立,求
成立,求![]() 的值;
的值;
(3)是否存在负数![]() ,使得
,使得![]() 是曲线
是曲线![]() 的切线.若存在,求出
的切线.若存在,求出![]() 的所有值:若不存在,请说明理由.
的所有值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com