设数列{
an}的前n项和为Sn=2
n+1-2,{
bn }是公差不为0的等差数列,其中
b2、
b4、
b9依次成等比数列,且
a2=
b2(1)求数列{
an }和{
bn}的通项公式: (2)设
cn=
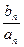
,求数列{
cn)的前n项和T
n
(1)n>1时,a。= S
n- S
n-1 =2
n+1-2-(2
n-2)=2
n 又n=1时,a
1=S
1=4-2=2,也符合上式,
故a
n=2
n(n∈矿),是首项为2公比为2的等比数列
设数列{
bn}的首项为b
1,公差为d (d≠0),由b
2=a
2=4,又
b2、
b4、
b9依次成等比数列得(4+2d)
2=4(4+7d),得d=3,b
1=I,故b
n=3n-2。
(2)T
n=
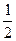
+
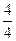
+
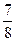
4+…+
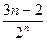
2T
n=1+
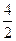
+

+
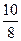
+…
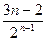
两式相减T
n = l+3(
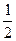
+
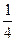
+

+…+
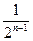
)-
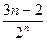
=1+3(
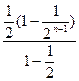
) -
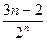
=1+3(1-
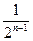
)-
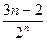
= 4-
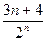
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知实数列
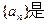
等比数列,其中
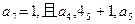
成等差数列.
(1)求数列
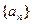
的通项公式;
(2)数列
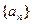
的前
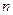
项和记为
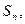
证明:
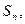
<128
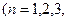
…).
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题


(本题满分14分)已知公差不为0的等差数列

的首项

为

(

),且
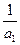
,

,

成等比数列(Ⅰ)求数列

的通项公式(Ⅱ)对

,试比较

与
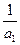
的大小.&
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
.(本小题满分12分)已知数列
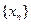
满足:
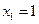
,

.
(I)证明:
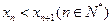
;
(II)证明:
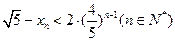
查看答案和解析>>

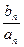 ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
 名校课堂系列答案
名校课堂系列答案