
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
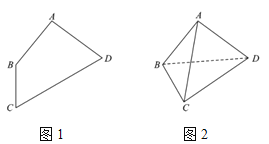
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在图1中,根据平面几何知识可得BC=1且∠CBD=90°,在图2中可以得到AC2=AB2+CB2,从而可证明BC⊥平面ABD从而可证明结论.
(2)由(1)有![]() ,用等体积法有
,用等体积法有![]() .
.
证明:法1:由左图知,![]()
在△BDC中,∠CBD=135°-45°=90°,
∠BDC=75°-45°=30°,
![]() ,所以BC=1,
,所以BC=1,
又在右图中,因为AC![]() ,AB=AD
,AB=AD![]() ,所以AC2=AB2+CB2
,所以AC2=AB2+CB2
所以BC⊥AB
又因为∠CBD=90°,所以BC⊥平面ABD
所以BC⊥AD
法2:如右图,设BD的中点为O,连结A0,CO,因为∠A=90°,AB=AD![]()
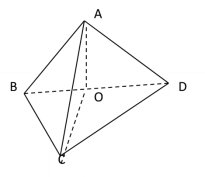
则![]()
由左图知,在△BDC中,∠CBD=135°-45°=90°
∠BDC=75°-45°=30°,所以BC=1,所以![]()
又因为AC![]() ,所以AC2=AO2+CO2
,所以AC2=AO2+CO2
所以AO⊥CO,所以AO⊥平面BCD,所以平面ABD⊥平面BCD,又∠CBD=90°
所以BC⊥平面ABD, 所以BC⊥AD
(2)因为AB=AD![]() ,AC
,AC![]() ,CD2=BC2+BD2=4
,CD2=BC2+BD2=4
所以CD2=AC2+AD2,所以AC⊥AD
设三棱锥B-ADC的高为h,则
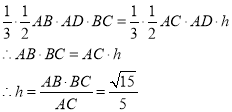


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上不重合的四点,
是椭圆上不重合的四点,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,且
,且![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)某同学发现:总存在正实数![]() ,
,![]() ,使
,使![]() ,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出
,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出![]() 的取值范围(不需要解答过程).
的取值范围(不需要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了
配方)做实验,各生产了![]() 件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
频数 |
|
|
|
|
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)若从![]() 配方产品中有放回地随机抽取
配方产品中有放回地随机抽取![]() 件,记“抽出的
件,记“抽出的![]() 配方产品中至少
配方产品中至少![]() 件二级品”为事件
件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(2)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: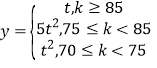 ,其中
,其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5名男生和4名女生中选出4人参加辩论比赛.
(1)如果男生中的甲与女生中的乙至少要有1人在内,那么有多少种不同选法?
(2)如果4个人中既有男生又有女生,那么有多少种不同选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高衡水市的整体旅游服务质量,市旅游局举办了旅游知识竞赛,参赛单位为本市内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游3名,其中高级导游1名.从这6名导游中随机选择2人参加比赛.
(1)求选出的2名都是高级导游的概率;
(2)为了进一步了解各旅游协会每年对本地经济收入的贡献情况,经多次统计得到,甲旅游协会对本地经济收入的贡献范围是![]() (单位:万元),乙旅游协会对本地经济收入的贡献范围是
(单位:万元),乙旅游协会对本地经济收入的贡献范围是![]() (单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
(单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com