练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知a=cos61°•cos127°+cos29°•cos37°，$b=\frac{{2tan{{13}°}}}{{1+{{tan}^2}{{13}°}}}$，$c=\sqrt{\frac{{1-cos{{50}°}}}{2}}$，则a，b，c的大小关系是（　　）
    A．a＜b＜cB．a＞b＞cC．c＞a＞bD．a＜c＜b

    分析 利用诱导公式，两角差的正弦函数公式，二倍角的正切函数公式化简，进而利用正弦函数的单调性及单位圆即可得解．

    解答 解：∵a=cos61°•cos127°+cos29°•cos37°=-cos61°•sin37°+sin61°•cos37°=sin（61°-37°）=sin24°，
    $b=\frac{{2tan{{13}°}}}{{1+{{tan}^2}{{13}°}}}$=sin26°，
    $c=\sqrt{\frac{{1-cos{{50}°}}}{2}}$=sin25°，
    ∴由y=sinx在（0°，90°）单调递增，利用单位圆的知识可得：sin24°＜sin25°＜sin26°＜tan26°，
    ∴a＜c＜b．
    故选：D．

    点评 本题主要考查了诱导公式，两角差的正弦函数公式，二倍角的正切函数公式，正弦函数的单调性的综合应用，考查了转化思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．函数f（x）=a|log2x|+1（a≠0），定义函数F（x）=$\left\{\begin{array}{l}{f（x），x＞0}\\{f（-x），x＜0}\end{array}\right.$，给出下列命题：
    ①F（x）=|f（x）；   
    ②函数F（x）是偶函数；
    ③当a＜0时，若0＜m＜n＜1，则有F（m）-F（n）＜0成立；
    ④当a＞0时，函数y=F（x）-2有4个零点．
    其中正确命题的序号为②③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是（　　）
    A．至少有一个白球；至少有一个红球B．至少有一个白球；红、黑球各一个
    C．恰有一个白球；一个白球一个黑球D．至少有一个白球；都是白球

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知$|{\vec a}|=1$，$|{\vec b}|=2$，$\vec a（\vec a-\vec b）=3$则$\vec a$与$\vec b$的夹角为（　　）
    A．$\frac{π}{3}$B．$\frac{π}{6}$C．$\frac{π}{2}$D．π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设Sn是数列的前n项和，已知a1=3，an+1=2Sn+3（n∈N*）．
    （1）求数列{an}的通项公式；
    （2）令bn=（2n-1）an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

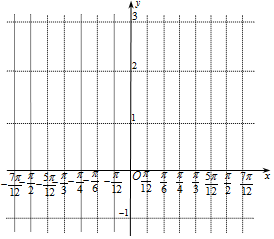    3．某同学用“五点法”画函数$f（x）=2sin（2x-\frac{π}{3}）+1$在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上的图象时，列表并填入了部分数据，如表：
    2x-$\frac{π}{3}$-$\frac{4}{3}$π-π-$\frac{π}{2}$0$\frac{π}{2}$$\frac{2}{3}$π
    x-$\frac{π}{2}$-$\frac{π}{3}$-$\frac{π}{12}$$\frac{π}{6}$$\frac{5π}{12}$$\frac{π}{2}$
    f（x）
    （1）请将上表数据补充完整，并在给出的直角坐标系中，画出f（x）在区间[-$\frac{π}{2}$，$\frac{π}{2}$]上的图象；
    （2）求f（x）的最小值及取最小值时x的集合；
    （3）求f（x）在$x∈[0，\frac{π}{2}]$时的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．要把半径为半圆形木料截成长方形，为了使长方形截面面积最大，则图中的α=（　　）
    A．$\frac{π}{4}$B．$\frac{π}{3}$C．$\frac{5π}{12}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设有序集合对（A，B）满足：A∪B={1，2，3，4，5，6，7，8}，A∩B=∅，记CardA，CardB分别表示集合A、B的元素个数，则符合条件CardA∉A，CardB∉B的集合的对数是44．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知a、b、c∈R，a＞b＞c，a+b+c=0，若实数x，y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x+y≤4}\\{bx+ay+c≥0}\end{array}\right.$，则目标函数z=2x+y（　　）
    A．有最大值，无最小值B．无最大值，有最小值
    C．有最大值，有最小值D．无最大值，无最小值

    查看答案和解析>>

    同步练习册答案