
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为等边三角形,E,F分别为
为等边三角形,E,F分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() .
.
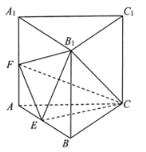
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)通过计算可得![]() ,通过证明
,通过证明![]() 平面
平面![]() ,可得
,可得![]() ,再根据直线与平面垂直的判定定理可得
,再根据直线与平面垂直的判定定理可得![]() 平面
平面![]() ;
;
(2)先说明直线![]() ,
,![]() ,
,![]() 两两垂直,再以
两两垂直,再以![]() ,
,![]() ,
,![]() 的方向为x,y,z轴的正方向,以点E为原点,建立空间直角坐标系,然后利用空间向量可求得结果.
的方向为x,y,z轴的正方向,以点E为原点,建立空间直角坐标系,然后利用空间向量可求得结果.
(1)证明:设![]() ,∵
,∵![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∵点E为棱![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵三棱柱![]() 的侧面
的侧面![]() 为平行四边形,
为平行四边形,
∴四边形![]() 为矩形,
为矩形,
∵点F为棱![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵三棱柱的底面![]() 是正三角形,E为
是正三角形,E为![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() 相交,
相交,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)可知![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴三棱柱![]() 是正三棱柱,
是正三棱柱,
设![]() 的中点为M,则直线
的中点为M,则直线![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
分别以![]() ,
,![]() ,
,![]() 的方向为x,y,z轴的正方向,以点E为原点,建立如图所示的空间直角坐标系,
的方向为x,y,z轴的正方向,以点E为原点,建立如图所示的空间直角坐标系,
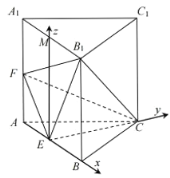
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则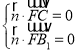 ,则
,则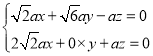 ,则
,则 ,
,
不妨取![]() ,则
,则![]() ,则
,则![]() ,所以
,所以![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则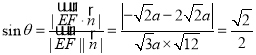 ,
,
因为![]() ,所以
,所以![]()
则直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,正三棱柱柱![]() 中底面边长为2,高为3,DE分别在
中底面边长为2,高为3,DE分别在![]() 与
与![]() 上,且
上,且![]() .
.
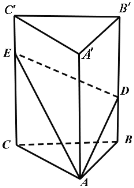
(1)AE上是否存在一点P,使得![]() 面
面![]() ?若不存在,说明理由;若存在,指出P的位置;
?若不存在,说明理由;若存在,指出P的位置;
(2)求点![]() 到截面ADE的距离.
到截面ADE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物商场分别推出支付宝和微信“扫码支付”购物活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用“扫码支付”.现统计了活动刚推出一周内每天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次,统计数据如下表所示:
表示每天使用扫码支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据散点图判断,在推广期内,扫码支付的人![]() 次关于活动推出天数
次关于活动推出天数![]() 的回归方程适合用
的回归方程适合用![]() 来表示,求出该回归方程,并预测活动推出第
来表示,求出该回归方程,并预测活动推出第![]() 天使用扫码支付的人次;
天使用扫码支付的人次;
(2)推广期结束后,商场对顾客的支付方式进行统计,结果如下表:
支付方式 | 现金 | 会员卡 | 扫码 |
比例 |
|
|
|
商场规定:使用现金支付的顾客无优惠,使用会员卡支付的顾客享受![]() 折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受
折优惠,扫码支付的顾客随机优惠,根据统计结果得知,使用扫码支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .现有一名顾客购买了
.现有一名顾客购买了![]() 元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
元的商品,根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用是多少?
参考数据:设![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: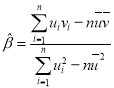 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校同时提供![]() 、
、![]() 两类线上选修课程,
两类线上选修课程,![]() 类选修课每次观看线上直播
类选修课每次观看线上直播![]() 分钟,并完成课后作业
分钟,并完成课后作业![]() 分钟,可获得积分
分钟,可获得积分![]() 分;
分;![]() 类选修课每次观看线上直播
类选修课每次观看线上直播![]() 分钟,并完成课后作业
分钟,并完成课后作业![]() 分钟,可获得积分
分钟,可获得积分![]() 分.每周开设
分.每周开设![]() 次,共开设
次,共开设![]() 周,每次均为独立内容,每次只能选择
周,每次均为独立内容,每次只能选择![]() 类、
类、![]() 类课程中的一类学习.当选择
类课程中的一类学习.当选择![]() 类课程
类课程![]() 次,
次,![]() 类课程
类课程![]() 次时,可获得总积分共_______分.如果规定学生观看直播总时间不得少于
次时,可获得总积分共_______分.如果规定学生观看直播总时间不得少于![]() 分钟,课后作业总时间不得少于
分钟,课后作业总时间不得少于![]() 分钟,则通过线上选修课的学习,最多可以获得总积分共________分.
分钟,则通过线上选修课的学习,最多可以获得总积分共________分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .以原点为极点,
.以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B.“![]() 为真命题”是“
为真命题”是“![]() 为真命题”的必要不充分条件
为真命题”的必要不充分条件
C.命题“![]()
![]() ”的否定是:“
”的否定是:“![]() 使得
使得![]() ”
”
D.命题p:“![]()
![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个笼子里关着![]() 只猫,其中有
只猫,其中有![]() 只白猫,
只白猫,![]() 只黑猫.把笼门打开一个小口,使得每次只能钻出
只黑猫.把笼门打开一个小口,使得每次只能钻出![]() 只猫.猫争先恐后地往外钻.如果
只猫.猫争先恐后地往外钻.如果![]() 只猫都钻出了笼子,以
只猫都钻出了笼子,以![]() 表示
表示![]() 只白猫被
只白猫被![]() 只黑猫所隔成的段数.例如,在出笼顺序为“□■□□□□■□□■”中,则
只黑猫所隔成的段数.例如,在出笼顺序为“□■□□□□■□□■”中,则![]() .
.
(1)求三只黑猫挨在一起出笼的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com