
【题目】如图,在长方体![]() 中,点
中,点![]() 分别在棱
分别在棱![]() 上,且
上,且![]() ,
,![]() .
.
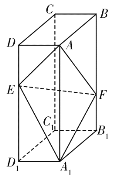
(1)证明:点![]() 在平面
在平面![]() 内;
内;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 、
、![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,进而可证得点
为平行四边形,进而可证得点![]() 在平面
在平面![]() 内;
内;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用空间向量法可计算出二面角
,利用空间向量法可计算出二面角![]() 的余弦值,进而可求得二面角
的余弦值,进而可求得二面角![]() 的正弦值.
的正弦值.
(1)在棱![]() 上取点
上取点![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
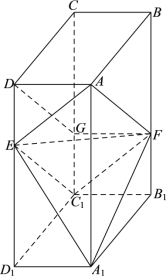
在长方体![]() 中,
中,![]() 且
且![]() ,
,![]() 且
且![]() ,
,
![]() ,
,![]() ,
,![]() 且
且![]() ,
,
所以,四边形![]() 为平行四边形,则
为平行四边形,则![]() 且
且![]() ,
,
同理可证四边形![]() 为平行四边形,
为平行四边形,![]() 且
且![]() ,
,
![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
因此,点![]() 在平面
在平面![]() 内;
内;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立如下图所示的空间直角坐标系
轴建立如下图所示的空间直角坐标系![]() ,
,
则![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由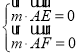 ,得
,得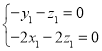 取
取![]() ,得
,得![]() ,则
,则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由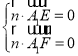 ,得
,得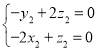 ,取
,取![]() ,得
,得![]() ,
,![]() ,则
,则![]() ,
,

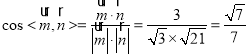 ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,![]() .
.
因此,二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为![]() ,则张师傅的材料利用率的最大值等于(注:材料利用率=
,则张师傅的材料利用率的最大值等于(注:材料利用率=![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】设球半径为R,圆柱的体积为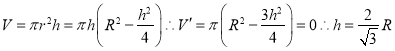 时圆柱的体积最大为
时圆柱的体积最大为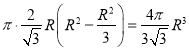 ,因此材料利用率=
,因此材料利用率=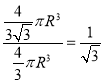 ,选C.
,选C.
点睛:空间几何体与球接、切问题的求解方法
求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
【题型】单选题
【结束】
12
【题目】已知抛物线![]() :
: ![]()
![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() :
: ![]() 相切,若动直线
相切,若动直线![]() 分别与曲线
分别与曲线![]() 、
、![]() 相交于
相交于![]() 、
、![]() 两点,则
两点,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=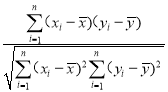 ,
,![]() ≈1.414.
≈1.414.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: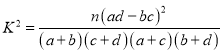 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定:![]() 三级为合格等级,
三级为合格等级,![]() 为不合格等级.
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
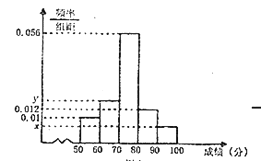
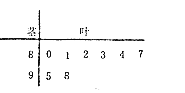
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,湖北省武汉市等多个地区发生新型冠状病毒感染的肺炎疫情.为了尽快遏制住疫情,我国科研工作者坚守在科研一线,加班加点争分夺秒与病毒抗争,夜以继日地进行研究.新型冠状病毒的潜伏期检测是疫情控制的关键环节之一.在传染病学中,通常把从致病刺激物侵入机体或对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期.钟南山院士带领的研究团队统计了武汉市某地区10000名医学观察者的相关信息,并通过咽拭子核酸检测得到1000名确诊患者的信息如下表格:
潜伏期(单位:天) |
|
|
|
|
人数 | 800 | 190 | 8 | 2 |
(1)求这1000名确诊患者的潜伏期样本数据的平均数![]() (同一组数据用该组数据区间的中点值代表).
(同一组数据用该组数据区间的中点值代表).
(2)新型冠状病毒的潜伏期受诸多因素影响,为了研究潜伏期与患者性别的关系,以潜伏期是否超过7天为标准进行分层抽样,从上述1000名患者中抽取100名,得到如下列联表.请将列联表补充完整,并根据列联表判断是否有90%的把握认为潜伏期与患者性别有关.
潜伏期≤7天 | 潜伏期>7天 | 总计 | |
男性患者 | 12 | ||
女性患者 | 50 | ||
总计 | 100 |
(3)由于采样不当标本保存不当采用不同类型的标本以及使用不同厂家试剂都可能造成核酸检测结果“假阴性”而出现漏诊.当核酸检测呈阴性时,需要进一步进行血清学![]() 抗体检测,以弥补核酸检测漏诊的缺点.现对10名核酸检测结果呈阴性的人员逐一地进行血清检测,记每个人检测出
抗体检测,以弥补核酸检测漏诊的缺点.现对10名核酸检测结果呈阴性的人员逐一地进行血清检测,记每个人检测出![]() (
(![]() 是近期感染的标志)呈阳性的概率为
是近期感染的标志)呈阳性的概率为![]() 且相互独立,设至少检测了9个人才检测出
且相互独立,设至少检测了9个人才检测出![]() 呈阳性的概率为
呈阳性的概率为![]() ,求
,求![]() 取得最大值时相应的概率
取得最大值时相应的概率![]() .
.
附: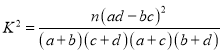 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为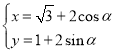 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,且长度单位相同.
轴的正半轴为极轴建立极坐标系,且长度单位相同.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() :
:![]() (
(![]() 为参数)被圆
为参数)被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆相交于点
的直线与椭圆相交于点![]() ,
,![]() 两点(两点均在
两点(两点均在![]() 轴的上方),且
轴的上方),且![]() ,
,![]()
(1)若![]() ,求椭圆的方程;
,求椭圆的方程;
(2)直线![]() 的斜率;
的斜率;
(3)求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com