
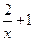 )=lgx,求f(x);
)=lgx,求f(x);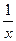 )=3x,求f(x).
)=3x,求f(x).科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 包.已知每次进货运输劳务费为62.5元,全年保管费为
包.已知每次进货运输劳务费为62.5元,全年保管费为 元.求:
元.求: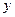 元表示为每次进货量
元表示为每次进货量 包的函数,并指
包的函数,并指查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
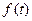 (万人)与时间
(万人)与时间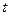 (天)的函数关系近似满足
(天)的函数关系近似满足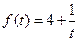 ,人均消费
,人均消费 (元)与时间
(元)与时间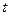 (天)的函数关系近似满足
(天)的函数关系近似满足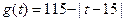 .(Ⅰ)求该城市的旅游日收益
.(Ⅰ)求该城市的旅游日收益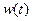 (万元)与时间
(万元)与时间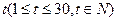 的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元).
的函数关系式;(Ⅱ)求该城市旅游日收益的最小值(万元). 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
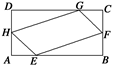
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 试问是否存在区间B(A∩B≠
试问是否存在区间B(A∩B≠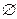 ),对于区间内任意实数x,只要n≥2,都有gn(x)<0.
),对于区间内任意实数x,只要n≥2,都有gn(x)<0. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com