练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某市组织了一次高二调研考试，考试后统计的数学成绩服从正态分布，其密度函数， x∈(－∞，＋∞)，则下列命题不正确的是( )

    A. 该市这次考试的数学平均成绩为80分

    B. 分数在120分以上的人数与分数在60分以下的人数相同

    C. 分数在110分以上的人数与分数在50分以下的人数相同

    D. 该市这次考试的数学成绩标准差为10

    【答案】B

    【解析】分析：根据密度函数的特点可得：平均成绩及标准差，再结合正态曲线的对称性可得分数在110分以上的人数与分数在50分以下的人数相同，从而即可选出答案.

    详解：密度函数，

    该市这次考试的数学平均成绩为80分

    该市这次考试的数学标准差为10，

    从图形上看，它关于直线对称，

    且50与110也关于直线对称，

    故分数在110分以上的人数与分数在50分以下的人数相同.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】有人用三段论进行推理：“函数 的导函数 的零点即为函数的极值点，函数 的导函数的零点为 ，所以 是函数 的极值点 ”，上面的推理错误的是（ ）

    A. 大前提 B. 小前提 C. 推理形式 D. 以上都是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，椭圆 的离心率为 ，顶点为A1、A2、B1、B2 ， 且 ．

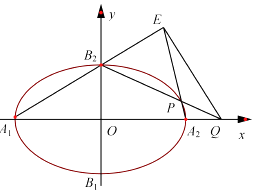
    （1）求椭圆C的方程；
    （2）P是椭圆C上除顶点外的任意点，直线B2P交x轴于点Q，直线A1B2交A2P于点E．设A2P的斜率为k，EQ的斜率为m，试问2m﹣k是否为定值？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若实数x，y满足2x﹣3≤ln（x+y+1）+ln（x﹣y﹣2），则xy= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC面积的大小为S，且3 =2S．
    （1）求sinA的值；
    （2）若C= ， =16，求AC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某射手射击1次，击中目标的概率是0.9，他连续射击4次，且他各次射击是否击中目标相互之间没有影响．有下列结论：

    ①他第3次击中目标的概率是0.9； ②他恰好击中目标3次的概率是0.93×0.1；

    ③他至少击中目标1次的概率是1－0.14 ④他恰好有连续2次击中目标的概率为3×0.93×0.1

    其中正确结论的序号是______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是矩形，面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC= ，M在PC上，且PA∥面BDM．
    （1）求直线PC与平面BDM所成角的正弦值；
    （2）求平面BDM与平面PAD所成锐二面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直三棱柱ABC-A1B1C1中，D,E分别是AB，BB1的中点.

    （Ⅰ）证明： BC1//平面A1CD;

    （Ⅱ）设AA1= AC=CB=2，AB=2，求三棱锥C一A1DE的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用长度分别为的四根木条围成一个平面四边形，则该平面四边形面积的最大值是____.

    查看答案和解析>>

    同步练习册答案