
【题目】已知双曲线x2﹣ ![]() =1,过点P(2,1)能否作一条直线l,与双曲线交于A,B两点,且点P是线段AB的中点?
=1,过点P(2,1)能否作一条直线l,与双曲线交于A,B两点,且点P是线段AB的中点?
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 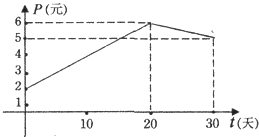
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI 是居民消费价格指数(consumer price index)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.下面是根据统计局发布的2017年1月一7月的CPI 同比增长与环比增长涨跌幅数据绘制的折线图.(注:2017 年2月与2016年2月相比较,叫同比;2017 年2 月与2017 年1月相比较,叫环比)根据该折线图,则下列结论错误的是( )
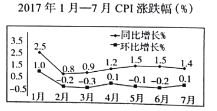
A. 2017 年1月一7月分别与2016年1月一7月相比较,CPI 有涨有跌
B. 2017 年1月一7月CPI 有涨有跌
C. 2017年1月一7月分别与2016年1月一7月相比较,1月CPI 涨幅最大
D. 2017 年2 月一7月CPI 涨跌波动不大,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=4y的焦点为F,过点F且斜率为1的直线与抛物线相交于M、N两点,设直线l是抛物线C的切线,且l∥MN,P为l上一点,则 ![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=x3+x-2在点P0处的切线l1平行于直线4x-y-1=0,且点P0在第三象限.
(1)求P0的坐标;(2)若直线l⊥l1,且l也过切点P0,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)解方程4x﹣2x﹣2=0.
(2)求不等式 log2(2x+3)>log2(5x﹣6);
(3)求函数y=( ![]() )
) ![]() ,x∈[0,5)的值域.
,x∈[0,5)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3|x|+log3|x|.
(1)判断函数的奇偶性,并加以证明;
(2)说明函数f(x)在(0,+∞)上的单调性,并利用单调性定义证明;
(3)若 f(2a)<28,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( ) 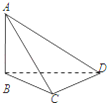
A.10 ![]() m
m
B.20m
C.20 ![]() m
m
D.40m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com