
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | $\frac{{1+\sqrt{2}}}{2}$ |
分析 确定抛物线y2=2px(p>0)的焦点与准线方程,利用点M为这两条曲线的一个交点,且|MF|=p,求出M的坐标,代入双曲线方程,即可求得结论.
解答 解:抛物线y2=2px(p>0)的焦点为F($\frac{p}{2}$,0),其准线方程为x=-$\frac{p}{2}$,
∵准线经过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左焦点,
∴c=$\frac{p}{2}$;
∵点M为这两条曲线的一个交点,且|MF|=p,
∴M的横坐标为$\frac{p}{2}$,
代入抛物线方程,可得M的纵坐标为±p,
将M的坐标代入双曲线方程,可得$\frac{\frac{{p}^{2}}{4}}{{a}^{2}}$-$\frac{{p}^{2}}{{b}^{2}}$=1,∴a=$\frac{\sqrt{2}-1}{2}$p,
∴e=$\frac{c}{a}$=1+$\sqrt{2}$.
故选:C.
点评 本题考查抛物线的几何性质,考查曲线的交点,考查双曲线的几何性质,确定M的坐标是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
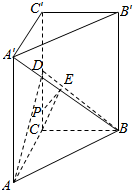 如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.
如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
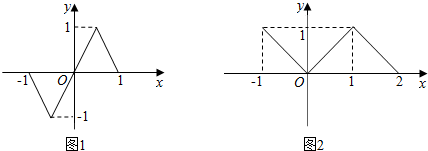
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
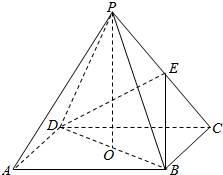 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
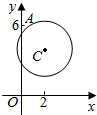 已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)
已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{5}\overrightarrow{OA}+\frac{2}{5}\overrightarrow{OB}$ | B. | $\frac{2}{5}\overrightarrow{OA}+\frac{3}{5}\overrightarrow{OB}$ | C. | $\frac{3}{5}\overrightarrow{OA}-\frac{2}{5}\overrightarrow{OB}$ | D. | $\frac{2}{5}\overrightarrow{OA}-\frac{3}{5}\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$a | B. | $\frac{3\sqrt{7}}{10}$a | C. | $\frac{3\sqrt{5}}{10}$a | D. | $\frac{7}{10}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或10 | B. | 10 | C. | 2 | D. | 4或8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com