
【题目】等比数列![]() 中,
中, ![]() 分别是下表中第
分别是下表中第![]() 行中的某一个数,且
行中的某一个数,且![]() 中任何两个数不在下表的同一列中.
中任何两个数不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列类比推理的结论正确的是( )
①类比“实数的乘法运算满足结合律”,得到猜想“向量的数量积运算满足结合律”;
②类比“平面内,同垂直于一直线的两直线相互平行”,得到猜想“空间中,同垂直于一直线的两直线相互平行”;
③类比“设等差数列{an}的前n项和为Sn , 则S4 , S8﹣S4 , S12﹣S8成等差数列”,得到猜想“设等比数列{bn}的前n项积为Tn , 则T4 , ![]() ,
, ![]() 成等比数列”;
成等比数列”;
④类比“设AB为圆的直径,p为圆上任意一点,直线PA,PB的斜率存在,则kPA . kPB为常数”,得到猜想“设AB为椭圆的长轴,p为椭圆上任意一点,直线PA,PB的斜率存在,则kPA . kPB为常数”.
A.①②
B.③④
C.①④
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△ABC中, ![]() ,
, ![]() ,点D是BC的中点. ( I)求证:
,点D是BC的中点. ( I)求证: ![]() ;
;
( II)直线l过点D且垂直于BC,E为l上任意一点,求证: ![]() 为常数,并求该常数;
为常数,并求该常数;
( III)如图2,若 ![]() ,F为线段AD上的任意一点,求
,F为线段AD上的任意一点,求 ![]() 的范围.
的范围.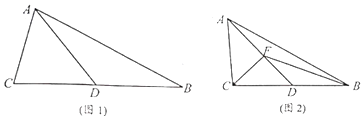
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣|x+a|
(1)当a=3时,解不等式f(x)≤ ![]() ;
;
(2)若关于x的不等式f(x)≤a解集为R,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.
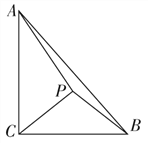
(1)若P是等腰直角三角形PBC的直角顶点,求PA的长;
(2)若∠BPC=![]() ,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
,设∠PCB=θ,求△PBC的面积S(θ)的解析式,并求S(θ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某著名歌星在某地举办一次歌友会,有1000人参加,每人一张门票,每张100元.在演出过程中穿插抽奖活动,第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个实数x,y(x,y∈[0,4]),若满足y≥ ![]() ,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
,电脑显示“中奖”,则抽奖者再次获得特等奖奖金;否则电脑显示“谢谢”,则不获得特等奖奖金.
(1)已知小明在第一轮抽奖中被抽中,求小明在第二轮抽奖中获奖的概率;
(2)设特等奖奖金为a元,小李是此次活动的顾客,求小李参加此次活动获益的期望;若该歌友会组织者在此次活动中获益的期望值是至少获得70000元,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com