
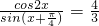 ,则sin2x的值为________.
,则sin2x的值为________.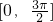 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线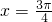 对称,当
对称,当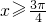 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________.
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为________. 满足
满足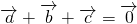 ,
,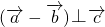 ,
, ,若
,若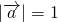 ,则
,则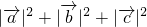 的值是________.
的值是________.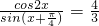 =
=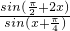 =
=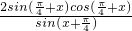 =2cos(
=2cos( +x),
+x), +x)=
+x)= ,∴sin2x=-cos(
,∴sin2x=-cos( +2x)=-[2
+2x)=-[2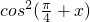 -1]=-(-
-1]=-(- )=
)= ,
, .
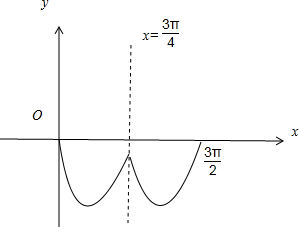
. ]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0.
]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得-1≤a≤0. <a≤0,f(x)=a有2个解,②当
<a≤0,f(x)=a有2个解,②当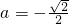 时,f(x)=a有3个解,
时,f(x)=a有3个解,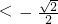 时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,
时,f(x)=a有4个交点,④a=-1时,f(x)=a有2个交点,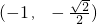 ,
,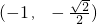 .
.
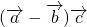 =
=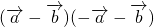 =0,∴
=0,∴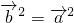 ,
, =
= .
.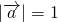 ,可得
,可得 =1.
=1. ,
, =-(
=-( ) 可得
) 可得 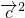 =
=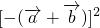 =
=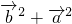 +2
+2 =2.
=2.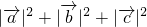 =4,
=4, +x)=
+x)= ,由sin2x=-cos(
,由sin2x=-cos( +2x),利用二倍角的余弦公式求出结果.
+2x),利用二倍角的余弦公式求出结果.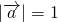 ,
, =1,再由得
=1,再由得 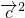 =
=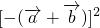 =
=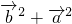 +2
+2 =2,即可求得值.
=2,即可求得值.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| a |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:022
填空题:
(1)
把所有单位向量的起点平移到一点O,则其终点构成的图形是______;(2)
已知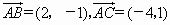 ,则
,则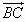 =_____________;
=_____________;
(3)
已知□ABCD的两条对角线相交于点O,以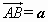 ,
,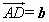 为基底向量,则
为基底向量,则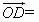 ________;
________;
(4)
若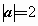 ,
,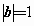 ,且
,且 ,则a与b的夹角为________;
,则a与b的夹角为________;
(5)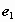
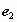 是单位向量,且
是单位向量,且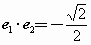 ,则
,则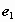 与
与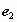 的夹角是___________.
的夹角是___________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| cos2x | ||
sin(x+
|
| 4 |
| 3 |
| 3π |
| 2 |
| 3π |
| 4 |
| 3π |
| 4 |
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| a |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市通州区潞河中学高一(上)期末数学试卷(解析版) 题型:解答题
 ,则sin2x的值为______.
,则sin2x的值为______. 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______
时,f(x)=cosx,如果关于x的方程f(x)=a有四个不同的解,则实数a的取值范围为______查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com