
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取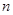 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在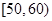 的学生人数为6.
的学生人数为6.
(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.
(1)75;(2)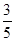
解析试题分析:(1)由直方图估计所抽取的数学成绩的众数,概率最大数学成绩的是在70-80之间,所以众数的估计值为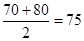 .
.
(2)由于其中成绩在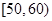 的学生人数为6,又在
的学生人数为6,又在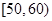 间的频率为0.12.所以总人数为50.由于成绩为
间的频率为0.12.所以总人数为50.由于成绩为 和
和 这两组的频率分别是0.24,0.16,所以这两组的抽取的人数分别为12,8人. 用分层抽样的方法这两组中共抽取5个学生,所以这两组分别抽取了3,2人. 从这5个学生中任取2人进行点评共有10种情况.其中分数在
这两组的频率分别是0.24,0.16,所以这两组的抽取的人数分别为12,8人. 用分层抽样的方法这两组中共抽取5个学生,所以这两组分别抽取了3,2人. 从这5个学生中任取2人进行点评共有10种情况.其中分数在 恰有1人的共有6种.所以即可求得结论.
恰有1人的共有6种.所以即可求得结论.
(1)由频率分布直方图可知:样本的众数为75. 3分
(2)由频率分布直方图可得:第三组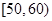 的频率:
的频率: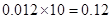 ,
,
所以 , 4分
, 4分 第四组
第四组 的频数:
的频数: ;
;
第五组 的频数:
的频数: ;
;
用分层抽样的方法抽取5份得:
第四组 抽取:
抽取: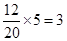 ;第五组
;第五组 抽取:
抽取: . 7分
. 7分
记抽到第四组 的三位同学为
的三位同学为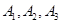 ,抽到第五组
,抽到第五组 的两位同学为
的两位同学为
则从5个同学中任取2人的基本事件有: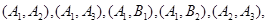
 ,
, ,共10种.
,共10种.
其中分数在 恰有1人有:
恰有1人有: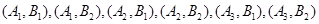 ,共6种.
,共6种. 所求概率:
所求概率: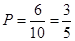 . 12分
. 12分
考点:1.统计图表的识别.2.统计图表中众数的估算.3.分层抽样.4.古典概型.


科目:高中数学 来源: 题型:解答题
某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分如图,据此解答下列问题: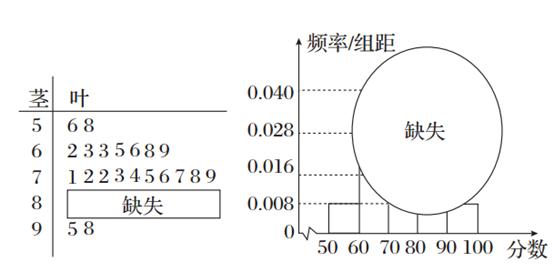
(1)求分数在[50,60]的频率及全班人数;
(2)求分数在[80,90]之间的频数,并计算频率分布直方图中[80,90]间的矩形的高.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少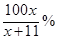 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小区统计部门随机抽查了区内 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过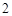 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过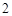 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为 .
.
(1)确定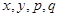 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这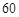 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取 人进行问卷调查,设
人进行问卷调查,设 为选取的
为选取的 人中“网购红人”的人数,求
人中“网购红人”的人数,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.下面是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图:
将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
| | 非积极分子 | 积极分子 | 合计 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛,其得分情况如茎叶图所示:
(1)若从甲运动员的不低于80且不高于90的得分中任选3个,求其中与平均得分之差的绝对值不超过2的概率;
(2)若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个,求甲、乙两名运动员得分之差的绝对值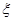 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 |  |  |  | 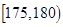 |  |  |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 智力评分 | 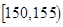 | 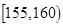 |  |  |  | 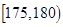 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班共有学生40人,将以此数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.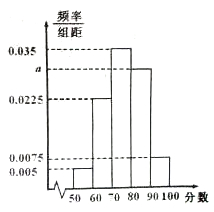
(1)请根据图中所给的数据,求a的值;
(2)从成绩在[50,70)内的学生中随机选3名学生,求这3名学生的成绩都在[60,70)内的概率;
(3)为了了解学生这次考试的失分情况,从成绩在[50,70)内的学生中随机选取3人的成绩进行分析,用X表示所选学生成绩在[60,70)内的人数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com