
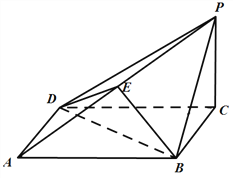
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,点
为正方形,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ) 设![]() ,试判断平面
,试判断平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,写出
能否成立;若成立,写出![]() 的一个值(只需写出结论).
的一个值(只需写出结论).
【答案】(Ⅰ)见解析; (Ⅱ)见解析(Ⅲ) 不能成立.
【解析】试题分析:
(1)由题意可得EO// PC,利用线面平行的判定定理可得PC//平面BDE;
(2) 利用题意证得PC⊥AC,PC⊥BD,结合线面垂直的判定定理即可证得结论;
(3)由空间关系可知面面垂直的关系不能成立.
试题解析:
证明:(Ⅰ)证明:设![]() ,连接
,连接![]() ,
,
因为底面![]() 为正方形,
为正方形,
所以![]() 是
是![]() 的中点,又点
的中点,又点![]() 是棱
是棱![]() 的中点,
的中点,
所以EO是的![]() 中位线,
中位线,
所以EO// PC
因为EO![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以PC//平面BDE;
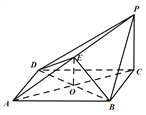
(Ⅱ)证明:(法一)在![]() 和
和![]() 中,
中,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ≌
≌![]() ,又点
,又点![]() 是棱
是棱![]() 的中点,
的中点,
所以![]() ,
,
所以![]()
因为平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
所以EO⊥AC,EO⊥BD,
因为EO//PC
所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以PC⊥平面ABCD.

(法二)连接PO
因为底面ABCD是正方形,
所以O是BD的中点,BD⊥AC,又PB=PD,
所以PO⊥BD,又PO∩AC=O,PO![]() 平面PAC,AC
平面PAC,AC![]() 平面PAC
平面PAC
所以BD⊥平面PAC
又OE![]() 平面PAC, 所以BD⊥OE,
平面PAC, 所以BD⊥OE,
因为平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
所以EO⊥AC,EO⊥BD,
因为OE∥PC,
所以PC⊥AC,PC⊥BD,又AC∩BD=O
所以所以PC⊥平面ABCD.
(Ⅲ) 不能成立


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() , 若
, 若![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的最短距离为
的最短距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
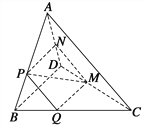
【题目】如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为________ (填序号).
①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线PM与BD所成的角为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
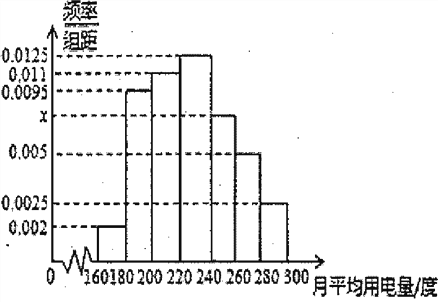
【题目】某城市100户居民的月平均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如下图示.
(Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:cm)满足关系
(单位:cm)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com