
(1)求动点P(x,y)的轨迹方程;
(2)过点M(0,3),作直线l与曲线C交于A,B两点,设ON=OA+OB,问是否存在直线l,使得四边形OANB为矩形?若存在,求出l的方程;若不存在,请说明理由.
解:(1)∵i=(1,0),j=(0,1),|a|+|b|=8,∴![]() =8,
=8,
即点P(x, y)到点(0,—2)与点(0,2)的距离之和为8.
设F1(0,—2),F2(0,2),∴|F 1F2|=4,|PF1|+|PF2|=8>|F1F2|,
由椭圆定义知点P的轨迹C是以F1.F2为焦点的椭圆.
∵2a=8, 2c=4,∴a=4, c=2,∴b2=a2—c2=12,
∴所求轨迹C方程为![]() =1.
=1.
(2)∵![]() ,∴OANB是平行四边形.
,∴OANB是平行四边形.
∵l过点M(0,3),若l是y轴,则A,B是椭圆的顶点,此时![]() =0,
=0,
∴N与O重合,这与四边形是平行四边形矛盾.所以直线l的斜率k必存在.
设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2),
若存在直线l使得OANB是矩形,则,OA![]() OB∴
OB∴![]() =0,即x1x2+y 1y2=0.
=0,即x1x2+y 1y2=0.
而y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9,
∴(1+k2)x1x2+3k(x1+x2)+9=0①
由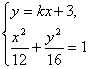 消去y,得(3k2+4)x2+18kx—21=0②
消去y,得(3k2+4)x2+18kx—21=0②
∵Δ=(18k)2—4(3k2+4)(—21)=(18k)2+84(3k2+4)>0,
∴方程②必有两实根x1.x2,且x1+x2=![]() ,x1x2=
,x1x2=![]() ,代入①得,
,代入①得,
-(1+k2)![]() =0,解得k2=
=0,解得k2=![]() ,
,
∴k=±![]() .所以存在符合题意的直线l,其方程为:
.所以存在符合题意的直线l,其方程为:
y=![]() 或y=
或y=![]() x+3.
x+3.


科目:高中数学 来源: 题型:
| 1 |
| x+2 |
| an |
| i |
| an |
| A0A1 |
| A1A2 |
| A2A3 |
| An-1An |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:013
设向量i=(0,1),![]() =λi,且P到A(3,-2)的距离是5,则实数λ等于( ).
=λi,且P到A(3,-2)的距离是5,则实数λ等于( ).
A.2
B.-6
C.2或-6
D.-2或6
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=x![]() +
+![]() ,A0为坐标原点,An为函数y=f(x)图象上横坐标为
,A0为坐标原点,An为函数y=f(x)图象上横坐标为
n(n∈N*)的点,向量an=![]() ,向量i=(1,0),设θn为向量an与向量i的夹角,满足
,向量i=(1,0),设θn为向量an与向量i的夹角,满足![]() tanθk<
tanθk<![]() 的最大整数n是( )
的最大整数n是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com