
����Ŀ�������¸߿��ĸ�IJ������룬����ѧ�����Ĺ滮Խ��Խ�ܵ����Ĺ�ע.һЩ�����Ѿ���ʼ���Կ���ѧ�����Ĺ滮ѡ�γ̣���ȡ����һ���ijɹ�.�±�Ϊij����Ϊ�˵���ѧ���ɼ���ѡ�����Ĺ滮�γ̵Ĺ�ϵ�������ȡ50��ѧ����ͳ������.
�ɼ����� | �ɼ��������� | �ܼ� | |
ѡ�����Ĺ滮�� | 15 | 10 | 25 |
��ѡ�����Ĺ滮�� | 6 | 19 | 25 |
�ܼ� | 21 | 29 | 50 |
���������������ö����Լ����˼�뷽���ܷ���![]() �İ�����Ϊ��ѧ���ijɼ��Ƿ�������ѡ�����Ĺ滮���йء�����˵�����ɣ�
�İ�����Ϊ��ѧ���ijɼ��Ƿ�������ѡ�����Ĺ滮���йء�����˵�����ɣ�
���������ȫУѡ�����Ĺ滮�ε�ѧ��������س�ȡ3��ѧ������鵽�ɼ����������ѧ������![]() �ķֲ��к���ѧ��������Ƶ�ʵ������ʼ��㣩.
�ķֲ��к���ѧ��������Ƶ�ʵ������ʼ��㣩.
�������
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
�ο���ʽ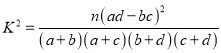 ������
������![]() .
.
���𰸡������а��գ����ɼ����������ֲ��м�������![]() .
.
��������
���������������Ĺ�ʽ���![]() ��ֵ��Ȼ����ݲο����������жϼ��ɣ�
��ֵ��Ȼ����ݲο����������жϼ��ɣ�
������������������ȫУѡ�����Ĺ滮�ε�ѧ���������ȡ1��ѧ���ɼ�����ĸ��ʣ��ɼ�������ĸ��ʣ������ж�![]() ��ȡֵΪ0��1��2��3�����ݶ���ֲ������ʽ�����⼴��.
��ȡֵΪ0��1��2��3�����ݶ���ֲ������ʽ�����⼴��.
����������֪��![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() .
.
������![]() �İ�����Ϊ��ѧ���ijɼ��������Ƿ�ѡ�����Ĺ滮���йء�.
�İ�����Ϊ��ѧ���ijɼ��������Ƿ�ѡ�����Ĺ滮���йء�.
����������֪��ȫУѡ�����Ĺ滮�ε�ѧ���������ȡ1��ѧ���ɼ�����ĸ���Ϊ![]() ���ɼ�������ĸ���Ϊ
���ɼ�������ĸ���Ϊ![]() ��
��
![]() ��ȡֵΪ0��1��2��3.
��ȡֵΪ0��1��2��3.
![]()
![]()
![]()
![]()
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ��
��![]() .
.


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1������![]() ��ֵ��ĸ�����
��ֵ��ĸ�����
��2����![]() ������ʽ
������ʽ![]() ���������
���������![]() Ϊ����ʱ����
Ϊ����ʱ����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ�Ȳ����У�
Ϊ�Ȳ����У�![]() ��
��![]() ������
������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ������
������![]() .
.
��1����![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��
��![]() ����ʹ
����ʹ![]() ������
������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ
��Բ![]() ��ֱ��l����
��ֱ��l����![]() ��
��
![]() ��ֱ��l��Բ
��ֱ��l��Բ![]() ���صõ��ҳ�Ϊ
���صõ��ҳ�Ϊ![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
![]() ��ԲP����
��ԲP����![]() Ϊֱ����Բ����ԲP��Բ
Ϊֱ����Բ����ԲP��Բ![]() �Ĺ���������ֱ�߷��̣�
�Ĺ���������ֱ�߷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��������M��4����2����N��2��4����
��1����MN�Ĵ�ֱƽ���߷��̣�
��2��ֱ��l������A��3��0��������ֱ��MNƽ�У���ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() �������ڵ㣨0��3����Բ���ھ����㣨2��1����㣨��2����3����ֱ��
�������ڵ㣨0��3����Բ���ھ����㣨2��1����㣨��2����3����ֱ��![]() �ϣ�
�ϣ�
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2��Բ![]() ��Բ
��Բ![]() ��
��![]() �ཻ��M��N���㣬����Բ�Ĺ�����MN�ij���
�ཻ��M��N���㣬����Բ�Ĺ�����MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ᳫ�����н�Լ�������˷�����ij��ͨ���������100���Ա�ͬ�ľ����Ƿ��������������ж����õ�������������
| ���������������ж� | �������������ж� |
�� | 45 | 10 |
Ů | 30 | 15 |
������ �� ������
�� ������
|
|
|
|
|
|
|
|
���ո������õ�����ȷ�����ǣ� ��
A.�ڷ�����ĸ��ʲ�����![]() ��ǰ���£���Ϊ�����о����ܷ�����
��ǰ���£���Ϊ�����о����ܷ�����![]() ����
����![]() �ж����Ա��й���
�ж����Ա��й���
![]() ��ǰ���£���Ϊ�����о����ܷ�����
��ǰ���£���Ϊ�����о����ܷ�����![]() ����
����![]() �ж����Ա�����
�ж����Ա�����
C.��![]() ���ϵİ�����Ϊ�����о����ܷ�����
���ϵİ�����Ϊ�����о����ܷ�����![]() ����
����![]() �ж����Ա��й���
�ж����Ա��й���
D.��![]() ���ϵİ�����Ϊ�����о����ܷ�����
���ϵİ�����Ϊ�����о����ܷ�����![]() ����
����![]() �ж����Ա�����
�ж����Ա�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������![]() �У���
����![]() ����
����![]() �ϵ�һ�����㣬ƽ��
�ϵ�һ�����㣬ƽ��![]() ����
����![]() �ڵ�
�ڵ�![]() �������������⣺
�������������⣺
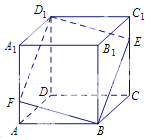
�ٴ��ڵ�![]() ��ʹ��
��ʹ��![]() //ƽ��
//ƽ��![]() ��
��
����������ĵ�![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��
�����ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��
��
�ܶ�������ĵ�![]() ������
������![]() �����������.
�����������.
������ȷ����������______����д��������ȷ�������ţ�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com