
【题目】为监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取10个零件,度量其内径尺寸(单位:![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的内径尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的内径尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示某一天内抽取的10个零件中其内径尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及X的数学期望;
及X的数学期望;
(2)某天正常工作的一条生产线数据记录的茎叶图如下图所示:

①计算这一天平均值![]() 与标准差
与标准差![]() ;
;
②一家公司引进了一条这种生产线,为了检查这条生产线是否正常,用这条生产线试生产了5个零件,度量其内径分别为(单位:![]() ):95,103,109,112,119,试问此条生产线是否需要进一步调试,为什么?
):95,103,109,112,119,试问此条生产线是否需要进一步调试,为什么?
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;
;![]() (2)①
(2)①![]()
![]() ;
;![]()
![]() .②需要进一步调试,理由见解析.
.②需要进一步调试,理由见解析.
【解析】
(1)根据![]() 原则,可求得当
原则,可求得当![]() 和
和![]() 时的概率,结合对立事件的概率关系即可求得
时的概率,结合对立事件的概率关系即可求得![]() ;由正态分布的期望公式即可求得X的数学期望.
;由正态分布的期望公式即可求得X的数学期望.
(2)根据茎叶图,列出数据即可求得平均值![]() ,由方差公式先求得
,由方差公式先求得![]() ,再求得标准差
,再求得标准差![]() ;由正态分布的
;由正态分布的![]() 原则,计算出
原则,计算出![]() .观测5个零件与该范围关系,即可判断是否需要进一步调试.
.观测5个零件与该范围关系,即可判断是否需要进一步调试.
(1)由题意![]()
则![]()
![]()
所以![]()
所以![]()
由题意可知![]()
则![]()
(2)①由茎叶图可得10个数据为:96,96,99,99,102,102,104,104,105,113
则平均值![]()
![]()
![]()
由参考数据可得![]()
![]()
②需要进一步调试,理由如下:
由①可知,若生产线正常工作,则![]() 服从正态分布
服从正态分布![]()
则![]()
可知零件落在![]() 之内的概率为
之内的概率为![]() ,落在
,落在![]() 之外的概率为
之外的概率为![]()
而![]()
由![]() 原则可知生产线异常,需进一步调试
原则可知生产线异常,需进一步调试


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]()
![]() ,P为AB上一动点,
,P为AB上一动点,![]() 交于AC于点D,现将
交于AC于点D,现将![]() 沿PD翻折至
沿PD翻折至![]() ,使平面
,使平面![]() 平面PBCD.
平面PBCD.
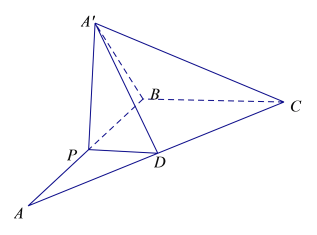
(1)若![]() ,求棱锥
,求棱锥![]() 的体积;
的体积;
(2)若点P为AB的中点,求证:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 | 3 | 4 | 5 | 6 | 7 | 8 |
销量 | 70 | 65 | 62 | 59 | 56 |
|
已知![]() .
.
(1)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个,求“好数据”至少
个,求“好数据”至少![]() 个的概率.
个的概率.
(参考公式:线性回归方程中![]() ,
,![]() 的估计值分别为
的估计值分别为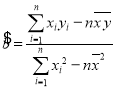 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 四所高校中选2所.
四所高校中选2所.
(1)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(2)若甲必选![]() ,记
,记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 校的人数,求随机变量
校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
某商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(2)求![]() 的分布列
的分布列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com