设数列{an}的前n项和为Sn,且Sn2-2Sn-anSn+1=0,n=1,2,3,….
(1)求a1,a2,a3;
(2)求Sn的表达式.
解:(1)当n=1时,由已知得

∴a
1=

同理,可解得 a
2=

,a
3=

(5分)
(2)解法一:由题设S
n2-2S
n-a
nS
n+1=0,
当n≥2时,a
n=S
n-S
n-1代入上式,得S
n-1S
n-2S
n+1=0,(*) (6分)
由(1)可得

,S
2=a
1+a
2=
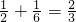
由(*)式可得
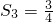
由此猜想:
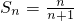
(8分)
证明:①当n=1时,结论成立.
②假设当n=k时结论成立,
即
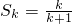
那么,由(*)得
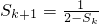
∴
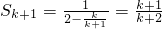
所以当n=k+1时结论也成立,根据①和②可知,
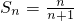
对所有正整数n都成立.(12分)
解法二:由题设S
n2-2S
n-a
nS
n+1=0,
当n≥2,a
n=S
n-S
n-1代入上式,得S
nS
n-1-2S
n+1=0
∴
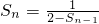
∴
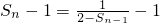
=
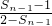
∴

=
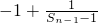
∴数列{
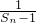
}是以
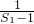
=-2为首项,以-1为公差的等差数列,
∴
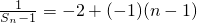
=-n-1
∴
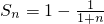
=

(12分)
分析:(1)把n=1,n=2,n=3分别代入已知递推公式即可求解a
1,a
2,a
3;
(2)解法一:由题设S
n2-2S
n-a
nS
n+1=0,利用n≥2时,a
n=S
n-S
n-1,代入整理可求S
1,S
2,S
3,然后猜想S
n,利用数学归纳法进行证明即可
解法二:由题设S
n2-2S
n-a
nS
n+1=0,利用n≥2,a
n=S
n-S
n-1代入整理,得S
nS
n-1-2S
n+1=0,然后构造等差数列
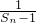
,根据等差数列的通项公式可求
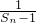
,进而可求
点评:本题主要考查了利用数列的递推公式求解数列的项及和,解法二中的构造等差数列进行求解通项公式的方法要注意体会掌握



 ,a3=
,a3= (5分)
(5分) ,S2=a1+a2=
,S2=a1+a2=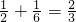 由(*)式可得
由(*)式可得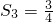
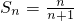 (8分)
(8分)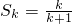 那么,由(*)得
那么,由(*)得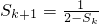
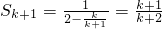
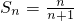 对所有正整数n都成立.(12分)
对所有正整数n都成立.(12分)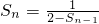
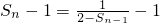 =
=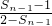
 =
=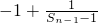
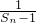 }是以
}是以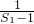 =-2为首项,以-1为公差的等差数列,
=-2为首项,以-1为公差的等差数列,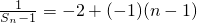 =-n-1
=-n-1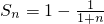 =
= (12分)
(12分)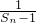 ,根据等差数列的通项公式可求
,根据等差数列的通项公式可求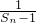 ,进而可求
,进而可求
