
【题目】已知函数![]() 的定义域为
的定义域为![]() ,满足
,满足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 时,
时,![]() .
.
①求![]() 时
时![]() 的表达式;
的表达式;
②若对任意![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度![]() (米
(米![]() 是时刻
是时刻![]() ,单位:时)的函数,记作:
,单位:时)的函数,记作:![]() ,下表是某日各时刻的浪高数据:
,下表是某日各时刻的浪高数据:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
经长期观测,![]() 的曲线可近似地看成是函数
的曲线可近似地看成是函数![]() ,
,![]() ,
,![]() 的图象.
的图象.
(![]() 的最小正周期
的最小正周期![]() ,振幅
,振幅![]() 及函数表达式;
及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的![]() 至
至![]() 之间,那个时间段不对冲浪爱好者开放?
之间,那个时间段不对冲浪爱好者开放?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,经过点
,经过点![]() 过点
过点![]() 的直线l与椭圆C相交于A,B两点,且与椭圆C的左准线交于点N.
的直线l与椭圆C相交于A,B两点,且与椭圆C的左准线交于点N.
![]() 求椭圆C的标准方程;
求椭圆C的标准方程;
![]() 当
当![]() 时,求直线l的方程;
时,求直线l的方程;
![]() 设
设![]() ,求
,求![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.
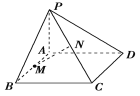
(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,则阳马
,则阳马![]() 的外接球的表面积是( )
的外接球的表面积是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/30/1913191114645504/1914064210190336/STEM/70d44ba6321c44a9bcc99e6010bf5643.png]
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤![]() (x+2)2成立.
(x+2)2成立.
(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-![]() x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y=![]() 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资![]() 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每![]() 长造价
长造价![]() 元,两侧墙砌砖,每
元,两侧墙砌砖,每![]() 长造价
长造价![]() 元,
元,
(1)求该仓库面积![]() 的最大值;
的最大值;
(2)若为了使仓库防雨,需要为仓库做屋顶.顶部每![]() 造价
造价![]() 元,求仓库面积
元,求仓库面积![]() 的最大值,并求出此时正面铁栅应设计为多长?
的最大值,并求出此时正面铁栅应设计为多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com