【题目】如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF（该矩形区域内无其他信号来源，基站工作正常）．若在该矩形区域内随机地选一地点，则该地点无信号的概率是（ ）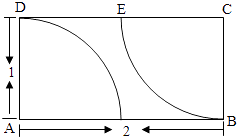
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】一个盒中装有编号分别为
的四个形状大小完全相同的小球．
（1）从盒中任取两球，求取出的球的编号之和大于
的概率．
（2）从盒中任取一球，记下该球的编号
，将球放回，再从盒中任取一球，记下该球的编号
，求
的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时，轮船位于港口
北偏西
且与该港口相距20海里的
处，并以30海里/时的航行速度沿正东方向匀速行驶，假设该小船沿直线方向以
海里/时的航行速度匀速行驶，经过
小时与轮船相遇.
（1）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？
（2）假设小艇的最高航行速度只能达到30海里/时，试设计航行方案（即确定航行方向与航行速度的大小），使得小艇能以最短时间与轮船相遇，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线C：y2=4x 的焦点为F．
（1）点A，P满足 
．当点A在抛物线C上运动时，求动点P的轨迹方程；
（2）在x轴上是否存在点Q，使得点Q关于直线y=2x的对称点在抛物线C上？如果存在，求所有满足条件的点Q的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在2016年6月英国“脱欧”公投前夕，为了统计该国公民是否有“留欧”意愿，该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民，调查统计他们是赞成“留欧”还是反对“留欧”．现已得知50人中赞成“留欧”的占60%，统计情况如下表：
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
（1）请补充完整上述列联表；
（2）请问是否有97．5%的把握认为赞成“留欧”与年龄层次有关？请说明理由．
参考公式与数据：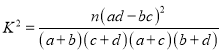
，其中
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
， 
，函数
，函数
在
轴上的截距我
，与
轴最近的最高点的坐标是
．
（Ⅰ）求函数
的解析式；
（Ⅱ）将函数
的图象向左平移
（
）个单位，再将图象上各点的纵坐标不变，横坐标伸长到原来的2倍，得到函数
的图象，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设某校新、老校区之间开车单程所需时间为
，只与道路畅通状况有关，对其容量为
的样本进行统计，结果如图：
| 25 | 30 | 35 | 40 |
频数（次） | 20 | 30 | 40 | 10 |
（1）求的分布列与数学期望
；
（2）刘教授驾车从老校区出发，前往新校区做一个50分钟的讲座，结束后立即返回老校区，求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组一次为[20，40），[40，60），[60，80），[80，100）．若低于60分的人数是15人，则该班的学生人数是（ ）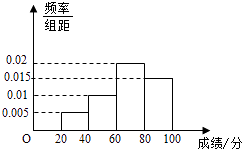 
A.45
B.50
C.55
D.60
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
