
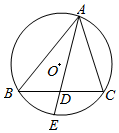
 如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.
如图,⊙O是△ABC的外接圆,AD平分∠BAC交BC于D,交△ABC的外接圆于E.分析 (1)过D作DM∥AB交AC于M,连接BE,利用平行线的性质,结合三角形的角平分线性质,即可得证;
(2)先求出DC,再利用三角形相似得出AD•(AD+DE)=AB•AC,即可求AD的长.
解答 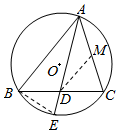 (1)证明:如图,过D作DM∥AB交AC于M,连接BE.
(1)证明:如图,过D作DM∥AB交AC于M,连接BE.
∴$\frac{BD}{DC}=\frac{AM}{MC}①$
又∵AD平分∠BAC,∴∠BAD=∠CAD,
又DM∥AB,∴∠BAD=∠ADM,∴∠CAD=∠ADM.
∴AM=MD.
∴$\frac{MD}{AB}=\frac{CM}{AC}⇒\frac{AB}{AC}=\frac{MD}{CM}=\frac{AM}{CM}②$,
由①②知$\frac{AB}{AC}=\frac{BD}{DC}$…(5分)
(2)解:∵AD•DE=BD•DC,
又$\frac{AB}{AC}=\frac{BD}{DC}⇒DC=\frac{2×1}{3}=\frac{2}{3}$,
∵△ADC∽△ABE.
∴$\frac{AD}{AB}=\frac{AC}{AE}$,∴AD•AE=AB•AC,
∴AD•(AD+DE)=AB•AC,
∴$A{D^2}=AB•AC-AD•DE=AB•AC-BD•DC=3×2-1×\frac{2}{3}=6-\frac{2}{3}=\frac{16}{3}$,
∴$AD=\frac{{4\sqrt{3}}}{3}$…(10分)
点评 本题考查平行线的性质,三角形的角平分线性质,考查三角形相似性质的运用,属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,f(x0)=0或g(x0)=0 | B. | ?x0∈R,f(x0)=0且g(x0)=0 | ||
| C. | ?x∈R,f(x)=0或g(x)=0 | D. | ?x∈R,f(x)=0且g(x)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{e}$) | B. | (0,$\frac{1}{e}$) | C. | (-∞,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
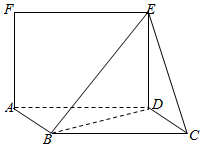 如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.
如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-∞,-2)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
| A. | (1,0) | B. | (2,2) | C. | ($\frac{7}{2}$,$\frac{13}{6}$) | D. | (3,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com