
【题目】如图所示,在多面体A1B1D1-DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点 ,过A1 , D,E的平面交CD 1于F。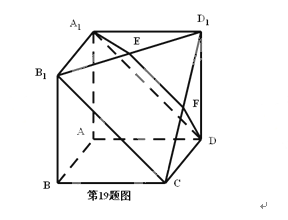
(1)证明:EF∥B1C
(2)求二面角E-A1D-B1的余弦。
【答案】
(1)
证明:依据正方形的性质可知A1B1//AB//DC,且A1B1=AB=DC,从而A1B1CD为平行四边形,则B1C//A1D,根据线面平行的判断定理知B1C//面A1DE,再由线面平行性质定理知EF//B1C.
(2)
解:因为四边形AA1B1B,ADD1A1,ABCD均为正方形,所以AA1![]() AB,AA1
AB,AA1![]() AD,AD
AD,AD![]() AB,且AA1=AB=AD,可以建以A为原点,分别为
AB,且AA1=AB=AD,可以建以A为原点,分别为![]() ,
,![]() ,
,![]() 为x轴,y轴,z轴单位正向量的平面直角坐标系,写出相关点的坐标,设出面A1DE的法向量
为x轴,y轴,z轴单位正向量的平面直角坐标系,写出相关点的坐标,设出面A1DE的法向量![]() =(r1,s1,t1)由此得r1,s1,t1应满足方程组
=(r1,s1,t1)由此得r1,s1,t1应满足方程组![]() ,(-1,1)尾气中一组解,所以可取
,(-1,1)尾气中一组解,所以可取![]() =(-1,1,1),同理A1B1CD的法向量
=(-1,1,1),同理A1B1CD的法向量![]() =(0,1,1)所以结合图形知二面角E-A1D-B的余弦值
=(0,1,1)所以结合图形知二面角E-A1D-B的余弦值
=![]()
【解析】
(2)因为四边形AA1B1B,ADD1A1,ABCD均为正方形,所以AA1![]() AB,AA1
AB,AA1![]() AD,AD
AD,AD![]() AB,且AA1=AB=AD,可以建以A为原点,分别为
AB,且AA1=AB=AD,可以建以A为原点,分别为![]() ,
,![]() ,
,![]() 为x轴,y轴,z轴单位正向量的平面直角坐标系,写出相关点的坐标,设出面A1DE的法向量
为x轴,y轴,z轴单位正向量的平面直角坐标系,写出相关点的坐标,设出面A1DE的法向量![]() =(r1,s1,t1)由此得r1,s1,t1应满足方程组
=(r1,s1,t1)由此得r1,s1,t1应满足方程组![]() ,(-1,1)为其中一组解,所以可取
,(-1,1)为其中一组解,所以可取![]() =(-1,1,1),同理A1B1CD的法向量
=(-1,1,1),同理A1B1CD的法向量![]() =(0,1,1)所以结合图形知二面角E-A1D-B的余弦值
=(0,1,1)所以结合图形知二面角E-A1D-B的余弦值
=![]() 。
。
【考点精析】关于本题考查的向量语言表述线面的垂直、平行关系,需要了解要证明一条直线和一个平面平行,也可以在平面内找一个向量与已知直线的方向向量是共线向量即可;设直线![]() 的方向向量是
的方向向量是![]() ,平面
,平面![]() 内的两个相交向量分别为
内的两个相交向量分别为![]() ,若
,若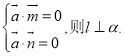 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】若a,b 是函数![]() 的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
的两个不同的零点,且a,b,-2 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·北京)某校老年、中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体状况,在抽取的样本
中,青年教师有320人,则该样本的老年教师人数为( )
A.90
B.100
C.180
D.300
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)设函数![]() ,
,![]() 的定义域均为
的定义域均为![]() ,且
,且![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,![]() ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(Ⅰ)求![]() ,
,![]() 的解析式,并证明:当
的解析式,并证明:当![]() 时,
时,![]() ,
,![]() ;
;
(Ⅱ)设![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同直线,![]() ,
,![]() 是两个不同平面,则下列命题正确的是
是两个不同平面,则下列命题正确的是
A.若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B.若m,n平行于同一平面,则m与n平行
C.若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D.若m,n不平行,则m与n不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设fn(x)是等比数列1,x,x2...,xn的各项和,其中x>0,n![]() N, ,n≥2,
N, ,n≥2,
(1)证明:函数Fn(x)=fn(x)-2在(![]() ,1)内有且仅有一个零点(记为xn),且xn=
,1)内有且仅有一个零点(记为xn),且xn=![]() +
+![]() xnn+1;
xnn+1;
(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)与gn(x)的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如图表: 
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下: ①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.试估计政府执行此计划的年度预算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com