
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取m个作为样本,称出它们的重量(单位:克),重量分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).
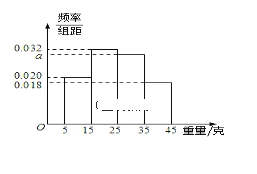
(1)根据样本数据,试估计盒子中小球重量的中位数与平均值(精确到0.01);
(2)从盒子装的大量小球中,随机抽取3个小球,其中重量在![]() 内的小球个数为
内的小球个数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中x的值;
(2)如果上学所需时间不少于1小时的学生可申请在学校住宿,若该学校有600名新生,请估计新生中有多少名学生可以申请住宿;
(3)由频率分布直方图估计该校新生上学所需时间的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,
中, ![]() 为正方形,
为正方形,![]() 是菱形,平面
是菱形,平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]()
![]() ;
;
(3)设点E,F,H,G分别是![]() 的中点,试判断
的中点,试判断![]() 四点是否共面,并说明理由.
四点是否共面,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC,P0是边AB上一定点,满足 ![]() ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有 ![]() 则( )
则( )
A.∠ABC=90°
B.∠BAC=90°
C.AB=AC
D.AC=BC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com