分析:(1)利用线面垂直的判定和性质定理及二面角的定义即可得出;
(2)利用正方形的性质、三角形全等、线面垂直的判定和性质即可证明;
(3)通过结论空间直角坐标系,利用点到平面的距离公式即可得出.
解答:解:(1)∵三棱柱ABC-A
1B
1C
1的侧棱与底面垂直,∴A
1A⊥AB,
又∵AC⊥AB,AC∩AA
1=A,
∴AB⊥平面ACC
1A
1,
∴AB⊥AM,
∴∠MAC即为二面角M-AB-C的平面角.
∵AC=1,则CM=
,∴AM=
=
.
∴
cos∠CAM==
.
(2)取AC的中点K,连接NK、A
1K.则NK∥AB.
由(1)可知:NK⊥平面ACC
1A
1.
∴NK⊥AM.
在正方形ACC
1A
1中,由△A
1AK≌△ACM,可得∠MAC=∠KA
1A,
∴
∠MAC+∠AKA1=90°,即AM⊥A
1K.
又NK∩A
1K=K,
∴AM⊥A
1PNK.
∴PN⊥AM.
(3)当λ=1时,假设线段AB上存在Q使得
VP-AQN=VP-AMN?点M到底面ANP的距离=2点Q到底面ANP的距离.下面通过建立空间直角坐标系来证明.
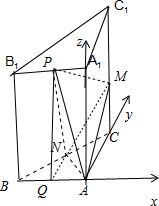
建立如图所示的坐标系.
则A(0,0,0),P
(-,0,1),
N(-,,0),M
(0,1,).
=(-,0,1),
=(-,,0),
=(0,1,).
设Q(0,k,0),则-1≤k≤0,
=(0,k,0).
设平面ANP的法向量为
=(x,y,z).
则
即
,令z=1,则x=y=2,
∴
=(2,2,1).
∴
=,得
2+=|2k|,解得
k=±,不满足条件-1≤k≤0,因此线段AB上不存在Q使得
VP-AQN=VP-AMN.
点评:熟练掌握线面垂直的判定和性质定理及二面角的定义、正方形的性质、三角形全等、三棱锥的条件计算公式、点到直线的距离公式是解题的关键.

 已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AB=AC=AA1=1,AB⊥AC,点M、N分别是CC1、BC的中点,动点P在线段A1B1上,且满足
已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AB=AC=AA1=1,AB⊥AC,点M、N分别是CC1、BC的中点,动点P在线段A1B1上,且满足


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案