
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过焦点且垂直于
,过焦点且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 所截得的弦长为
所截得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 是坐标原点,求
是坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据离心率以及弦长,结合![]() ,可知
,可知![]() ,可得结果.
,可得结果.
(2)假设点![]() 坐标,根据斜率存在与否假设直线方程,并与椭圆方程联立,使用韦达定理,表示出
坐标,根据斜率存在与否假设直线方程,并与椭圆方程联立,使用韦达定理,表示出![]() ,结合不等式,可得结果.
,结合不等式,可得结果.
解:(1)设椭圆![]() 的半焦距为
的半焦距为![]() .
.
因为过焦点且垂直于![]() 轴的直线交椭圆
轴的直线交椭圆
![]() 所得的弦长为
所得的弦长为![]() ,所以
,所以![]() ,
,
得![]() ①因为椭圆
①因为椭圆![]() 的离心率为
的离心率为![]() ,
,
所以![]() ②
②
又![]() ③
③
由①②③,解得![]() .
.
故椭圆![]() 的标准方程是
的标准方程是![]() .
.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,
直线![]() 的方程为
的方程为![]() ,联立
,联立
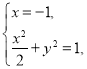 解得
解得 或
或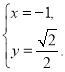
则点![]() 的坐标分别为
的坐标分别为
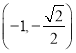 ,
,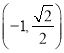 或
或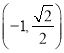 ,
,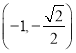 .
.
所以
 ;
;
当直线![]() 的斜率存在时,
的斜率存在时,
设直线![]() 的方程为
的方程为![]() .
.
联立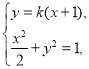 消去
消去![]()
得![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 的内部,
的内部,
所以直线![]() 与椭圆
与椭圆![]() 一定有两个不同的交点
一定有两个不同的交点![]() .
.
则![]() .
.
所以![]()
化简可得![]()
则![]()
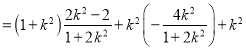
化简可得![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() ,
,
即![]() ,所以
,所以![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e-x,其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(-![]() +3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
+3x0)成立.试比较ea-1与ae-1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在频率分布直方图中,众数左边和右边的直方图的面积相等;
B.为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行編号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样;
C.“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
D.命题![]() :“
:“![]() ,使得
,使得![]() ”的否定为:“
”的否定为:“![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月18日,国务院办公厅发布了《生活垃圾分类制度实施方案》,我市环保部门组织了一次垃圾分类知识的网络问卷调查,每位市民都可以通过电脑网络或手机微信平台参与,但仅有一次参加机会工作人员通过随机抽样,得到参与网络问卷调查的100人的得分(满分按100分计)数据,统计结果如下表.
组别 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
(1)环保部门规定:问卷得分不低于70分的市民被称为“环保关注者”.请列出![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下,认为是否为“环保关注者”与性别有关?
的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.现在从本次调查的“环保达人”中利用分层抽样的方法随机抽取5名市民参与环保知识问答,再从这5名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“环保达人”又有女“环保达人”的概率.
附表及公式: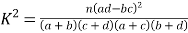 ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
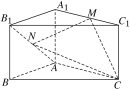
【题目】如图,在直三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,点M为A1C1的中点,点N为AB1上一动点.若点N为AB1的中点且CM⊥MN,求二面角MCNA的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著.下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图.下列描述错误的是( )
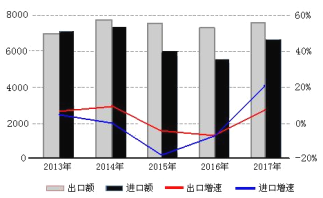
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: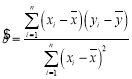 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com