
【题目】如图所示,边长为a的空间四边形ABCD中,∠BCD=90°,平面ABD⊥平面BCD,则异面直线AD与BC所成角的大小为( )
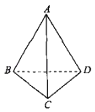
A. 30°B. 45°C. 60°D. 90°
【答案】C
【解析】
由题意得![]() ,
,![]() ,从而
,从而![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 为正方形,即有
为正方形,即有![]() ,从而
,从而![]() (或其补角)即为异面直线
(或其补角)即为异面直线![]() 与
与![]() 所成角,由此能求出异面直线
所成角,由此能求出异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
由题意得BC=CD=a,∠BCD=90°,
∴BD=![]() ,∴∠BAD=90°,
,∴∠BAD=90°,
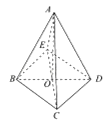
取BD中点O,连结AO,CO,
∵AB=BC=CD=DA=a,
∴AO⊥BD,CO⊥BD,且AO=BO=OD=OC=![]() ,
,
又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊥BD,
∴AO⊥平面BCD,
延长CO至点E,使CO=OE,连结ED,EA,EB,
则四边形BCDE为正方形,即有BC∥DE,
∴∠ADE(或其补角)即为异面直线AD与BC所成角,
由题意得AE=a,ED=a,
∴△AED为正三角形,∴∠ADE=60°,
∴异面直线AD与BC所成角的大小为60°.
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某中学高一期中考试结束后,从高一年级1000名学生中任意抽取50名学生,将这50名学生的某一科的考试成绩(满分150分)作为样本进行统计,并作出样本成绩的频率分布直方图(如图).
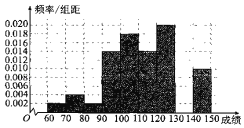
(1)由于工作疏忽,将成绩[130,140)的数据丢失,求此区间的人数及频率分布直方图的中位数;(结果保留两位小数)
(2)若规定考试分数不小于120分为优秀,现从样本的优秀学生中任意选出3名学生,参加学习经验交流会.设X表示参加学习经验交流会的学生分数不小于130分的学生人数,求X的分布列及期望;
(3)视样本频率为概率.由于特殊原因,有一个学生不能到学校参加考试,根据以往考试成绩,一般这名学生的成绩应在平均分左右.试根据以上数据,说明他若参加考试,可能得多少分?(每组数据以区问的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以平面直角坐标系xOy的原点为极点,x轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线l的坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为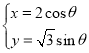 (θ为参数).
(θ为参数).
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)以曲线C上的动点M为圆心、r为半径的圆恰与直线l相切,求r的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的机器上存在一种易损元件,这种元件发生损坏时,需要及时维修. 现有甲、乙两名工人同时从事这项工作,下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 | 9日 | 10日 |
甲维修的元件数 | 3 | 5 | 4 | 6 | 4 | 6 | 3 | 7 | 8 | 4 |
乙维修的元件数 | 4 | 7 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 7 |
(1)从这![]() 天中,随机选取一天,求甲维修的元件数不少于5件的概率;
天中,随机选取一天,求甲维修的元件数不少于5件的概率;
(2)试比较这10天中甲维修的元件数的方差![]() 与乙维修的元件数的方差
与乙维修的元件数的方差![]() 的大小.(只需写出结论);
的大小.(只需写出结论);
(3)由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加几名工人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com