
【题目】已知函数f(x)=ax3+x2(a∈R)在x=﹣![]() 处取得极值.
处取得极值.
(1)确定a的值;
(2)讨论函数g(x)=f(x)ex的单调性.
【答案】(1) a=![]() ;(2) 在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.
;(2) 在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.
【解析】(1)对f(x)求导得f′(x)=3ax2+2x.
∵f(x)=ax3+x2(a∈R)在x=﹣![]() 处取得极值,∴f′(﹣
处取得极值,∴f′(﹣![]() )=0,
)=0,
∴3a![]() +2(﹣
+2(﹣![]() )=0,∴a=
)=0,∴a=![]() ;
;
(2)由(1)得g(x)=(![]() x3+x2)ex,
x3+x2)ex,
∴g′(x)=(![]() x2+2x)ex+(
x2+2x)ex+(![]() x3+x2)ex=
x3+x2)ex=![]() x(x+1)(x+4)ex,
x(x+1)(x+4)ex,
令g′(x)=0,解得x=0,x=﹣1或x=﹣4,
当x<﹣4时,g′(x)<0,故g(x)为减函数;
当﹣4<x<﹣1时,g′(x)>0,故g(x)为增函数;
当﹣1<x<0时,g′(x)<0,故g(x)为减函数;
当x>0时,g′(x)>0,故g(x)为增函数;
综上知g(x)在(﹣∞,﹣4)和(﹣1,0)内为减函数,在(﹣4,﹣1)和(0,+∞)为增函数.


科目:高中数学 来源: 题型:
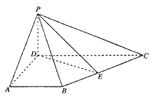
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为
,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轮船由甲地逆水匀速行驶至乙地,甲、乙两地相距s(km),水流速度为p(km/h),轮船在静水中的最大速度为q(km/h)(p,q为常数,且q>p),已知轮船每小时的燃料费用与轮船在静水中的速度v(km/h)成正比,比例系数为常数k.
(1)将全程燃料费用y(元)表示为静水中速度v(km/h)的函数;
(2)若s=100,p=10,q=110,k=2,为了使全程的燃料费用最少,轮船的实际行驶速度应为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数f(x)为增函数,且f(f(x))=4x+9,g(x)=mx+m+3(m∈R).
(1)当x∈[-1,2]时,若不等式g(x)>0恒成立,求m的取值范围;
(2)如果函数F(x)=f(x)g(x)为偶函数,求m的值;
(3)当函数f(x)和g(x)满足f(g(x))=g(f(x))时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加师大附中第30界田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根![]() 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班从6名班干部中(其中男生4人,女生2人),任选3人参加学校的义务劳动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com