练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．已知两圆相交于A（-1，3），B（-6，m）两点，且这两圆的圆心均在直线x-y+c=0上，则m+2c的值为（　　）
    A．-1B．26C．3D．2

    分析 由圆的性质可知，AB与x-y+c=0垂直且AB被x-y+c=0平分，可求KAB，从而可求m，然后由AB的中点在直线上可求c，结合选项可判断．

    解答 解：由圆的性质可知，AB与x-y+c=0垂直且AB被x-y+c=0平分，
    ∴KAB=$\frac{m-3}{-6+1}$=-1，
    ∴m=8，
    ∵AB的中点在直线上，
    ∴AB的中点（-$\frac{7}{2}$，$\frac{11}{2}$）代入方程得c=9，
    ∴m+2c=8+18=26．
    故选：B．

    点评 本题主要考查了两圆相交性质：两圆的公共弦被连心线垂直平分的应用，属于基础试题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．已知中心在原点，焦点在x轴上的椭圆C过点（1，$\frac{\sqrt{2}}{2}$），离心率为$\frac{{\sqrt{2}}}{2}$，A1，A2是椭圆C的长轴的两个端点（A2位于A1右侧），B是椭圆在y轴正半轴上的顶点．
    （1）求椭圆C的标准方程；
    （2）是否存在经过点（0，$\sqrt{2}$）且斜率为k的直线l与椭圆C交于不同两点P和Q，使得向量$\overrightarrow{OP}$+$\overrightarrow{OQ}$与$\overrightarrow{{A_2}B}$共线？如果存在，求出直线方程；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知全集U={1，2，3，4}，A={1，2}，则满足A⊆B的集合B个数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在复平面xOy内，若A（2，-1），B（0，3），则?OACB中，点C对应的复数为（　　）
    A．2+2iB．2-2iC．1+iD．1-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．在极坐标系中，已知A（2，$\frac{π}{6}$），B（4，$\frac{π}{3}$），则△AOB的面积S=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设函数f（x）在点x0附近有定义，且有f（x0+△x）-f（x0）=a△x+b（△x）2，其中a，b为常数，则（　　）
    A．f'（x）=aB．f'（x）=bC．f'（x0）=aD．f'（x0）=b

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

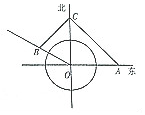    16．某化工厂O正东方向和北偏西60°方向分别有两条通向工厂的公路，工厂正北方向有一观察站C，OC=2千米，因化工厂原料泄漏，工厂周围1千米的范围内均有不同程度的影响．现准备从观察站C处修两条隔离绿化带CA，CB（其中A，B为隔离带与公路交接点）．且使CA⊥CB，隔离带与两条公路线围成的面积为S．
    （1）①若OA=a千米，试把S表示成a的函数．并写出其定义域；
    ②若∠OAC=θ，试把S表示成θ的函数，并写出其定义域；
    （2）选择上述两个函数中的以个，试求S的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知等差数列{an}的前n项和为Sn，a4=9，S3=15．
    （1）求Sn；
    （2）设数列$\{\frac{1}{S_n}\}$的前n项和为Tn，证明：${T_n}＜\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知$\frac{\overline z}{1+i}=2+i$，则复数z=（　　）
    A．1-3iB．-1-3iC．-1+3iD．1+3i

    查看答案和解析>>

    同步练习册答案