
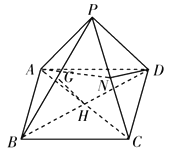
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)设![]() 分别为
分别为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]()
【解析】
(I)连接![]() ,利用平行四边形的性质,结合三角形的中位线,证得
,利用平行四边形的性质,结合三角形的中位线,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(II)取棱![]() 的中点
的中点![]() ,连接
,连接![]() ,根据等腰三角形的性质证得
,根据等腰三角形的性质证得![]() ,根据面面垂直的性质定理证得
,根据面面垂直的性质定理证得![]() 平面
平面![]() ,由此证得
,由此证得![]() ,再由
,再由![]() 证得
证得![]() 平面
平面![]() .
.
(III)连接![]() ,结合(II)中证得的
,结合(II)中证得的![]() 平面
平面![]() ,判断出
,判断出![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,解三角形求得线面角的正弦值.
所成的角,解三角形求得线面角的正弦值.
(Ⅰ)如图,连接![]() .
.
易知![]() ,
,![]() .
.
又由![]() ,
,
可知![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)如图,取棱![]() 的中点
的中点![]() ,连接
,连接![]() .
.
依题意,得![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)如图,连接![]() .
.
由(Ⅱ)中![]() 平面
平面![]() ,可知
,可知![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]() ,
,![]() ,且
,且![]() 为
为![]() 中点,
中点,
所以![]() .
.
又![]() ,在
,在![]() 中,
中,![]() ,
,
所以![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知命题![]() “存在
“存在![]() ”,命题
”,命题![]() :“曲线
:“曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆”,命题
轴上的椭圆”,命题![]() “曲线
“曲线![]() 表示双曲线”
表示双曲线”
(1)若“![]() 且
且![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 直线交x轴于点A,交y轴于点B,抛物线
直线交x轴于点A,交y轴于点B,抛物线![]() (
(![]() )经过点A,交x轴于另一点C,如图所示.
)经过点A,交x轴于另一点C,如图所示.
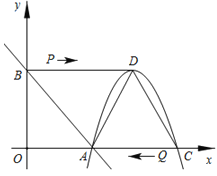
(1)求抛物线的解析式.
(2)设抛物线的顶点为D,连接BD,AD,CD,动点P在BD上以每秒2个单位长度的速度由点B向点D运动,同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当![]() 时,求t的值;
时,求t的值;
②过点E作![]() ,垂足为点M,过点P作
,垂足为点M,过点P作![]() 交线段AB或AD于点N,当
交线段AB或AD于点N,当![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是一个类似计步数据库的公众账号,现从“微信运动”的![]() 个好友(男、女各
个好友(男、女各![]() 人)中,记录了他们某一天的走路步数,并将数据整理如下表:
人)中,记录了他们某一天的走路步数,并将数据整理如下表:
0-2000步 | 2001-5000步 | 5001-8000步 | 8001-10000步 | >10000步 | |
男(人数) | 2 | 4 | 6 | 10 | 8 |
女(人数) | 1 | 7 | 10 | 9 | 3 |
(1)若某人一天的走路步数超过![]() 步被系统评定为“积极型”,否则评定为“懈怠型",根据题意完成下面的
步被系统评定为“积极型”,否则评定为“懈怠型",根据题意完成下面的![]() 列联表,并据此判断能否有
列联表,并据此判断能否有![]() %的把握认为“评定类型"与“性别“有关?
%的把握认为“评定类型"与“性别“有关?
积极型 | 懈怠型 | 总计 | |
男(人数) | |||
女(人数) | |||
总计 |
(2)现从被系统评定为“积极型”好友中,按男女性别分层抽样,共抽出![]() 人,再从这
人,再从这![]() 人中,任意抽出
人中,任意抽出![]() 人发一等奖,求发到一等奖的
人发一等奖,求发到一等奖的![]() 中恰有一名女性的概率.
中恰有一名女性的概率.
附:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天上学都需要经过一个有交通信号灯的十字路口.已知十字路口的交通信号灯绿灯亮的时间为40秒,黄灯5秒,红灯45秒.如果小明每天到路口的时间是随机的,则小明上学时到十字路口需要等待的时间不少于20秒的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() ,以动点
,以动点![]() 为圆心的圆经过点
为圆心的圆经过点![]() ,且圆
,且圆![]() 与圆
与圆![]() 内切.
内切.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com