
【题目】对于正三角形![]() ,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设
,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设![]() 是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设
是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设![]() 是第
是第![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第1次挖去的中间小三角形面积,
是第1次挖去的中间小三角形面积,![]() 是第2次挖去的三个小三角形面积之和),
是第2次挖去的三个小三角形面积之和),![]() 是前
是前![]() 次挖去的所有三角形的面积之和,则
次挖去的所有三角形的面积之和,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,(其中
,(其中![]() 为自然对数的底数,
为自然对数的底数,![]() …).
…).
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)若![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数且
为正整数且![]() ,将等式
,将等式![]() 记为
记为![]() 式.
式.
(1)求函数![]() ,
,![]() 的值域;
的值域;
(2)试判断当![]() 时(或2时),是否存在
时(或2时),是否存在![]() ,
,![]() (或
(或![]() ,
,![]() ,
,![]() )使
)使![]() 式成立,若存在,写出对应
式成立,若存在,写出对应![]() ,
,![]() (或
(或![]() ,
,![]() ,
,![]() ),若不存在,说明理由;
),若不存在,说明理由;
(3)求所有能使![]() 式成立的
式成立的![]() (
(![]() )所组成的有序实数对
)所组成的有序实数对![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组,
年龄段的人员进行了调查研究,将各年龄段人数分成5组,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
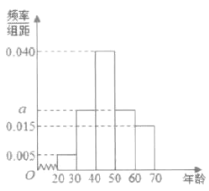
(Ⅰ)求图中的![]() 值;
值;
(Ⅱ)求被调查人员的年龄的中位数和平均数;
(Ⅲ)采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,在抽取的8人中随机抽取2人,则这2人都来自于第三组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某足球俱乐部对“一线队引援”和“青训”投入分别规划如下:2018年,该俱乐部在“一线队引援”投入资金为16000万元,“青训”投入资金为1000万元.计划每年“一线队引援”投入比上一年减少一半,“青训”投入比上一年增加一倍.
(1)请问哪一年该俱乐部“一线队引援”和“青训”投入总和最少?
(2)从2018年起(包括2018年)该俱乐部从哪一年开始“一线队引援”和“青训”总投入之和不低于62000万元?(总投入是指各年投入之和)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体![]() 中,已知
中,已知![]() ,
,![]() .
.

(1)求:凸多面体![]() 的体积;
的体积;
(2)若![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)若点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上滑动,且线段
上滑动,且线段![]() 的长恒等于
的长恒等于![]() ,线段
,线段![]() 的中点为
的中点为![]()
①试证:点![]() 必落在过线段
必落在过线段![]() 的中点
的中点![]() 且平行于底面
且平行于底面![]() 的平面上;
的平面上;
②试求点![]() 的轨迹.
的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:①对任意
满足:①对任意![]() ,存在正常数
,存在正常数![]() ,都有
,都有![]() 成立;②
成立;②![]() 的值域为
的值域为![]() (
(![]() ),则函数
),则函数![]() 是( )
是( )
A.周期为2的周期函数B.周期为4的周期函数
C.奇函数D.偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com