
 如图,正四棱柱ABCD-A1B1C1D1(即底面为正方形的直四棱柱)中,AA1=2AB=4,点 E 在 CC1 上且 C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1(即底面为正方形的直四棱柱)中,AA1=2AB=4,点 E 在 CC1 上且 C1E=3EC. 证明:如图,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,
证明:如图,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系, ,
, ,
, ,
, ,
, ,
, ,
,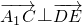 ,
, ,
, ,
, ,
, ,
, ,
, ,
,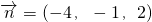 ,
, =(-2,2,-4),
=(-2,2,-4), ,
, >|=|
>|=| |=
|= ,
, .
. ,
, ,
, ,由向量法能够证明A1C丄平面BED.
,由向量法能够证明A1C丄平面BED. ,
, ,求出平面A1DE的法向量
,求出平面A1DE的法向量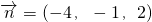 ,取
,取 =(-2,2,-4),
=(-2,2,-4), ,
, >|能求出直线A1C与平面A1DE所成角的正弦值.
>|能求出直线A1C与平面A1DE所成角的正弦值.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
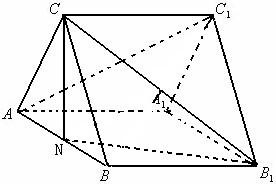 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.查看答案和解析>>
科目:高中数学 来源:2013届安徽省高二上学期期中考试理科数学 题型:解答题
(本小题满分12分)如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB的中点.
(1)求证:AC1∥平面CNB1;
(2)求四棱锥C-ANB1A1的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.查看答案和解析>>
科目:高中数学 来源:安徽省期中题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:安徽省期中题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com