
【题目】下列命题中正确的命题是( )
A.标准差越小,则反映样本数据的离散程度越大
B.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,则预报变量
每增加1个单位时,则预报变量![]() 减少0.4个单位
减少0.4个单位
C.对分类变量![]() 与
与![]() 来说,它们的随机变量
来说,它们的随机变量![]() 的观测值
的观测值![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
D.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
【答案】BD
【解析】
A选项,标准差越小,则反映样本数据的离散程度越小,即可判断出A不正确;B选项,在回归直线方程![]() 中,当解释变量x每增加1个单位时,根据斜率的意义即可判断;C选项,对分类变量X与Y来说,它们的随机变量
中,当解释变量x每增加1个单位时,根据斜率的意义即可判断;C选项,对分类变量X与Y来说,它们的随机变量![]() 的观测值k越小,“X与Y有关系”的把握程度越小,即可判断;选项D,根据残差平方和的意义即可判断.
的观测值k越小,“X与Y有关系”的把握程度越小,即可判断;选项D,根据残差平方和的意义即可判断.
标准差越小,则反映样本数据的离散程度越小,因此A不正确;
在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,
每增加1个单位时,
则预报变量![]() 减少0.4个单位,B正确;
减少0.4个单位,B正确;
对分类变量![]() 与
与![]() 来说,它们的随机变量
来说,它们的随机变量![]() 的观测值
的观测值![]() 越小,
越小,
“![]() 与
与![]() 有关系”的把握程度越小,因此C不正确;
有关系”的把握程度越小,因此C不正确;
在回归分析模型中,残差平方和越小,
说明模型的拟合效果越好,D正确.
故选:BD.


 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙三个盒子,其中每个盒子中都装有标号分别为1、2、3、4、5、6的六张卡片,现从甲、乙、丙三个盒子中依次各取一张卡片使得卡片上的标号恰好成等差数列的取法数为( )
A.14B.16C.18D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的定义域分别为
的定义域分别为![]() ,若存在常数
,若存在常数![]() ,满足:①对任意
,满足:①对任意![]() ,恒有
,恒有![]() ,且
,且![]() .②对任意
.②对任意![]() ,关于
,关于![]() 的不等式组
的不等式组![]()
![]() 恒有解,则称
恒有解,则称![]() 为
为![]() 的一个“
的一个“![]() 型函数”.
型函数”.
(1)设函数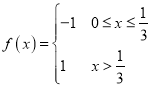 和
和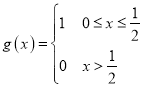 ,求证:
,求证:![]() 为
为![]() 的一个“
的一个“![]() 型函数”;
型函数”;
(2)设常数![]() ,函数
,函数![]() ,
,![]() .若
.若![]() 为
为![]() 的一个“
的一个“![]() 型函数”,求
型函数”,求![]() 的取值范围;
的取值范围;
(3)设函数![]() .问:是否存在常数
.问:是否存在常数![]() ,使得函数
,使得函数![]() 为
为![]() 的一个“
的一个“![]() 型函数”?若存在,求
型函数”?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市100000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
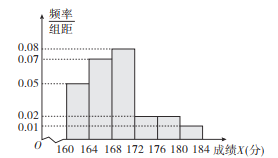
在频率分布直方图的分组中,以各组的区间中点值代表该组的各个值,测试成绩![]() 落入该区间的频率作为测试成绩取该区间中点值的概率.已知甲、乙两名学生的测试成绩分别为168分和170分.
落入该区间的频率作为测试成绩取该区间中点值的概率.已知甲、乙两名学生的测试成绩分别为168分和170分.
(1)求技能测试成绩![]() 的中位数
的中位数![]() ,对甲、乙的成绩作出客观的评价;
,对甲、乙的成绩作出客观的评价;
(2)若市教育局把这次技能测试看作技能大比武,且作出以下奖励规定:
给测试成绩![]() 者颁发奖金
者颁发奖金![]() 元,
元,
给测试成绩![]() 者颁发奖金元
者颁发奖金元![]() ,求
,求![]() ;
;
(3)若市教育局把这次技能看作是毕业过关测试,且作出以下规定:
当测试成绩![]() 时,统一交测试费和补测费300元;
时,统一交测试费和补测费300元;
当测试成绩![]() 时,统一交测试费100元;
时,统一交测试费100元;
当测试成绩![]() 时,免交测试费且颁发500元奖金.
时,免交测试费且颁发500元奖金.
若![]() ,据此统计:每个测试者平均最多应该交给教育局多少元?
,据此统计:每个测试者平均最多应该交给教育局多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com