
【题目】已知函数f(x)= ![]() .
.
(1)若函数f(x)在区间(a,a+ ![]() )(a>0)上存在极值点,求实数a的取值范围;
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】
(1)解:函数f(x)定义域为(0,+∞), ![]() f,
f,
由f′(x)=0x=1,当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,
则f(x)在(0,1)上单增,在(1,+∞)上单减,
所以函数f(x)在x=1处取得唯一的极值.
由题意得 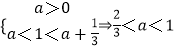 ,故所求实数a的取值范围为
,故所求实数a的取值范围为 ![]()
(2)解:当x≥1时,不等式 ![]() .
.
令 ![]() ,由题意,k≤g(x)在[1,+∞)恒成立.
,由题意,k≤g(x)在[1,+∞)恒成立. ![]()
令h(x)=x﹣lnx(x≥1),则 ![]() ,当且仅当x=1时取等号.
,当且仅当x=1时取等号.
所以h(x)=x﹣lnx在[1,+∞)上单调递增,h(x)≥h(1)=1>0
因此 ![]() ,则g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2
,则g(x)在[1,+∞)上单调递增,g(x)min=g(1)=2
所以k≤2,即实数k的取值范围为(﹣∞,2].
【解析】(1)求导数,确定函数f(x)在x=1处取得极大值,根据函数在区间(a,a+ ![]() )(a>0)上存在极值点,可得
)(a>0)上存在极值点,可得 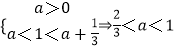 ,即可求实数a的取值范围;(2)当x≥1时,分离参数,构造
,即可求实数a的取值范围;(2)当x≥1时,分离参数,构造 ![]() ,证明g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,即可求实数k的取值范围.
,证明g(x)在[1,+∞)上是单调递增,所以[g(x)]min=g(1)=2,即可求实数k的取值范围.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)=a+ ![]() (a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
(a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
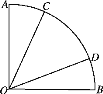
【题目】如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x﹣1)的图象关于点(1,0)对称,且当x∈(﹣∞,0),f(x)+xf′(x)<0成立.若a=(20.2)f(20.2),b=(ln2)f(ln2),c=(log2 ![]() )f(log2
)f(log2 ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足向量 ![]() =(cosA,cosB),
=(cosA,cosB), ![]() =(a,2c﹣b),
=(a,2c﹣b), ![]() ∥
∥ ![]() .
.
(1)求角A的大小;
(2)若a=2 ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x+4)=f(x),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣6,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,求实数a的取值范围是( )
)x﹣6,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,求实数a的取值范围是( )
A.(1,2)
B.(2,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),
=(﹣2,m), ![]() =
= ![]() +(t2+1)
+(t2+1) ![]() ,
, ![]() =﹣k
=﹣k ![]() +
+ ![]()
![]() ,m∈R,k、t为正实数.
,m∈R,k、t为正实数.
(1)若 ![]() ∥
∥ ![]() ,求m的值;
,求m的值;
(2)若 ![]() ⊥
⊥ ![]() ,求m的值;
,求m的值;
(3)当m=1时,若 ![]() ⊥
⊥ ![]() ,求k的最小值.
,求k的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
 附:
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆C1:(x﹣1)2+y2=2,圆C2:(x﹣m)2+(y+m)2=m2 . 圆C2上存在点P满足:过点P向圆C1作两条切线PA,PB,切点为A,B,△ABP的面积为1,则正数m的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com