
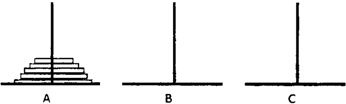
 ��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�
��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�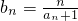 ��������{bn}��ǰn���Sn��
��������{bn}��ǰn���Sn�� =
= =
=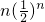 ��
�� +
+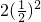 +
+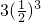 +��+
+��+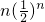 �٣�
�٣� sn=
sn=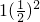 +
+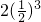 +
+ +��+
+��+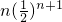 �ڣ�
�ڣ�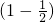 sn=
sn= +
+ +
+ +��+
+��+ -
-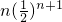 ��
��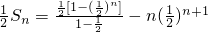 ��
��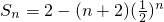 ��
��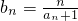 =
= =
=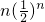 ������sn=
������sn= +
+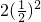 +
+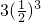 +��+
+��+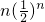 ����
���� sn=
sn=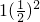 +
+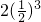 +
+ +��+
+��+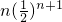 ����ʽ�������
����ʽ������� sn���Ӷ���sn��
sn���Ӷ���sn��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
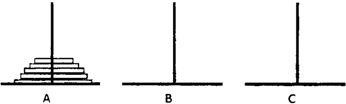 ��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�
��ŵ�������Ǹ���һ����˵�γɵ�һ�����⣺���������Ӻ�����һ�������ϵ����ɴ�С���ȵĴ���Բ�̣������й���Բ�̴�һ��������ȫ���Ƶ���һ�������ϣ�| n | an+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��ɽ��ʦ���и������ߴ����������ѧ�Ծ������ƣ��������棩 ���ͣ������
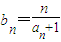 ��������{bn}��ǰn���Sn��
��������{bn}��ǰn���Sn��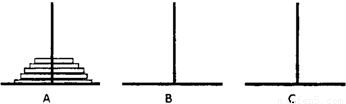
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com